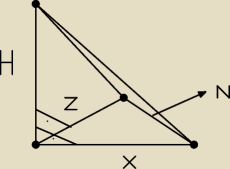
Objętość ostrosłupa ABCD. kleszcz: Podstawą ostrosłupa ABCD jest trójkąt ABC. Krawędź AD jest wysokością ostrosłupa (zobacz rysunek). Oblicz objętość ostrosłupa ABCD, jeśli wiadomo, że AD = 12, BC = 6, BD = CD = 13. https://www.google.pl/search?q=Podstaw%C4%85+ostros%C5%82upa+ABCS+jest+tr%C3%B3jk%C4%85t+ABC.+Kraw%C4%99d%C5%BA+AD+jest+wysoko%C5%9Bci%C4%85+ostros%C5%82upa+%28zobacz+rysunek%29.&biw=1366&bih=611&source=lnms&tbm=isch&sa=X&ei=adP5VMKBNoL1Urefg_gB&ved=0CAYQ_AUoAQ#imgrc=pvsaNOBQLG5x8M%253A%3BjBzYrYXCXkaONM%3Bhttp%253A%252F%252Fwww.matemaks.pl%252Fgrafika%252Fmatura05052010%252Fzadanie32.gif%3Bhttp%253A%252F%252Fwww.matemaks.pl%252Fplaylista-ostroslupy.html%3B188%3B225 W narysowanej podstawie: x=5(z Pitagorasa). z=5(z Pitagorasa). małe kropki to kąty proste. bok oznaczony strzałką − 6. I teraz mamy trzy boki: x=5 z=5 n=6 L=5+5+6=16. połowa obwodu − 8. P_p=√8(8−5)(8−5)(8−6)=√144=12 V=^12*12₃=48 ? Dobrze jest wszystko?

Mila: Dobrze.

kleszcz: ok, dzięki Mila.