 .
.
| √3 | ||
(2(10−b))2 = 2b2(1− | ) | |
| 2 |
| 1 | ||
S = | b·b·sin30° | |
| 2 |
| b2 | ||
S = | ||
| 4 |
 Zastanawiam się tylko, ponieważ to jest zadanie podstawy
i nie ma w podręczniku nic o twierdzeniu cosinusów
Zastanawiam się tylko, ponieważ to jest zadanie podstawy
i nie ma w podręczniku nic o twierdzeniu cosinusów  trochę mnie martwi, czy mogłoby się
znaleźć takie zadanie na maturze podstawowej z matmy, a np. widziałam taki sposób, że ktoś
zamiast liczyć do kąta 75stopni podzielił go sobie na 45stopni i 30stopni tez tak mozna?
Przy okazji chciałam się jeszcze zapytać o jedną rzecz:
mianowicie umiem sprawdzać, czy ciąg jest rosnący, stały czy malejący, ale czy da radę
sprawdzić czy jest nierosnący albo niemalejący?
trochę mnie martwi, czy mogłoby się
znaleźć takie zadanie na maturze podstawowej z matmy, a np. widziałam taki sposób, że ktoś
zamiast liczyć do kąta 75stopni podzielił go sobie na 45stopni i 30stopni tez tak mozna?
Przy okazji chciałam się jeszcze zapytać o jedną rzecz:
mianowicie umiem sprawdzać, czy ciąg jest rosnący, stały czy malejący, ale czy da radę
sprawdzić czy jest nierosnący albo niemalejący?

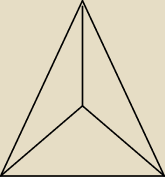 Jeżeli podzielisz trójkąt na trzy mniejsze − tak żeby kąt 75° był podzielony na 60° i 15°, to
wszystkie trzy odcinki wewnątrz trójkąta będą przystające (tworzą się trzy trójkąty
równoramienne o ramionach długości a). Stosując trzy razy ten wzór na pole trójkąta otrzymamy
(1) S = a2sin60° + 2·a2sin120°
− dostaniemy wzór na pole dużego trójkąta zależny tylko od a.
Stosując jeszcze raz wzór na pole dużego trójkata − tym razem o ramionach b i kacie miedzy nimi
30°otrzymamy
(2) S = b2sin30°
− wzór zależny tylko od b.
Porównanie (1) i (2) pozwoli znaleźć związek między a i b, drugi związek mamy w treści zadania:
a+2b = 20.
W ten sposób wyliczymy z układu równań a i b (potrzebna nam jest tylko jedna z tych liczb, np.
b, żeby ją podstawić do wzoru (2)).
Jeżeli podzielisz trójkąt na trzy mniejsze − tak żeby kąt 75° był podzielony na 60° i 15°, to
wszystkie trzy odcinki wewnątrz trójkąta będą przystające (tworzą się trzy trójkąty
równoramienne o ramionach długości a). Stosując trzy razy ten wzór na pole trójkąta otrzymamy
(1) S = a2sin60° + 2·a2sin120°
− dostaniemy wzór na pole dużego trójkąta zależny tylko od a.
Stosując jeszcze raz wzór na pole dużego trójkata − tym razem o ramionach b i kacie miedzy nimi
30°otrzymamy
(2) S = b2sin30°
− wzór zależny tylko od b.
Porównanie (1) i (2) pozwoli znaleźć związek między a i b, drugi związek mamy w treści zadania:
a+2b = 20.
W ten sposób wyliczymy z układu równań a i b (potrzebna nam jest tylko jedna z tych liczb, np.
b, żeby ją podstawić do wzoru (2)).