Twierdzenie sinusów
Jiley: 1. W trójkącie ABC są dane: |AB|=12cm, |<CAB|=30 stopni oraz |<ABC|=45 stopni. Oblicz długości
pozostałych boków trójkąta i promień okręgu opisanego na tym trójkącie.
2. W trójkącie ABC są dane: |AB|= 4cm, |BC|= 4√ 3/3 (4√ 3 − licznik, a 3 − mianownik) oraz
|<BAC|=30 stopni. Oblicz długość boku AC, długość promienia okręgu opisanego na tym trójkącie
oraz miary pozostałych jego kątów.
3. Balon znajdujący się na pewnej wysokości oraz dwa punkty A i B w terenie wyznaczają trójkąt
w płaszczyźnie prostopadłej do płaszczyzny terenu. Oblicz, na jakiej wysokości znajduję się
balon, jeśli kąty tego trójkąta przy podstawie długości 60m mają miary alfa=45 stopni i
beta=75 stopni.
Zadania są z tematu twierdzenie sinusów. Byłabym wdzięczna gdyby ktoś wytłumaczył mi krok po
kroku jak to zrobić
dero2005:
Narysuj sobie trójkąt ABC. Oznacz odcinek AB jako a, odcinek BC jako c odcinek CA jako b. Przy
wierzchołku A oznacz kąt 30
o, przy wierzchołku. B oznacz kąt 45
o, przy wierzchołku C oznacz
kąt α.
Suma kątów trójkąta wynosi 180
o. Więc
30 + 45 + α = 180
α = 105
o
Napisz wzór sinusów
| a | | b | | c | |
| = |
| = |
| = 2R |
| sinα | | sinβ | | sinγ | |
| 12 | | b | | c | |
| = |
| = |
| = 2R |
| sin105o | | sin45o | | sin30o | |
R − promień okręgu opisanego na trójkącie
Oblicz: sin 105
o = sin(60 + 45) = sin 60*cos 45 + sin 45*cos 60 =
R =
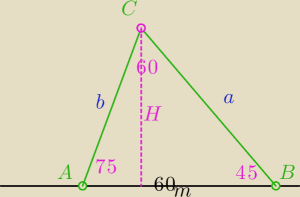3)
łatwo obliczysz, że kąt przy wierzchołku C ma miarę 60o
Z twierdzenia sinusów