Pole przez całkę mg: Witam, zadanie: Oblicz pole figury ograniczonej przez y=√x ; y=1/x ; y=2 narysowałem wykres, pole oznaczyłem pod prostą y=2, z dołu ograniczone przez pozostałe funkcje wyliczyłem punkty przecięcia, x=4 ; x=1/2 całka oznaczona od 4 do 1/2 z ∫(2 −1/x)dx ?

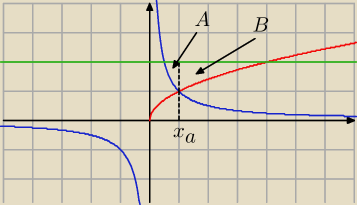
Draghan: Musisz policzyć sumę dwóch całek, całkę dla figury A + całkę dla figury B.

	1
Musisz jeszcze policzyć przecięcie funkcji y = √x i y =		, to jest na rysunku punkt
	x

x_a.

mg: Teraz rozumiem, trzeba policzyć osobno pola xa=1 Pa = całka od 1 do 1/2 z ∫(2−(1/x))dx ∫[2−(1/x)]dx = 2x − lnx +c po podstawieniu wynik ~3.69 Pb = całka od 4 do 1 z ∫(2−√x)dx ∫(2−√x)dx = 2x − (1/3)* x⁽3/2) +c po podstawieniu wynik 11/3 p= ~7.36 zgadza się ?

mg: * Pa pomyliłem znaki, Pa=0.31 p= ~3.98

J: zapisałeś granice całkowania odwrotnnie , nie wiem czy przynajmniej dobrze liczysz

	1
PA: <		,1>
	2

P_B <1,4>

mg: podstawiam poprawnie

J:

	1		2
w drugiej całce masz		... ma być:
	3		3

mg: masz rację. wtedy drugie pole wychodzi 4/3, suma pól ~1.64