proszę o rozwi,ązanie Michał: Dane są dwa punkty A = (−1, 0) i B = (1 , 0) Udowodnij że zbiór punktów P spełniających warunek IAPI = 2 *IBPI jest okręgiem

Eta: P(x,y) , A(−1,0) , B(1,0) |AP|²=4|BP|² (x+1)²+y²=4(x−1)²+4y² ..........

	10		5		16
x2+y2−		x+1=0 ⇔ o: (x−		)2+y2=
	3		3		9

Michał: nie przyszło mi na myśl podnieść do kwadratu dziękuję bardzo

Eta:

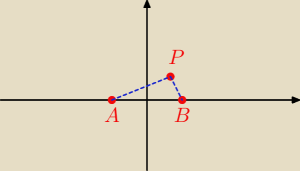Janek191:: P = ( x ; y) A = ( − 1; 0) B = ( 1 ; 0) I AP I = √( x + 1)² + ( y − 0)² = √ x² + 2 x + 1 + y² I BP I = √( x − 1)² + ( y − 0)² = √ x² − 2 x + 1 + y² więc I AP I = 2 I BP I zapiszemy √ x² + 2 x + 1 + y² = 2*√ x² − 2 x + 1 + y² ; podnosimy do kwadratu x² + 2 x + 1 + y² = 4 x² − 8 x + 4 + 4 y² 3 x² − 10 x + 3 y² + 3 = 0 / : 3

	10
x2 −		x + y2 + 1 = 0
	3

	5		25
( x −		)2 −		+ ( y − 0)2 = − 1
	3		9

	5		16
( x −		)2 + ( y − 0)2 =
	3		9

	5		4
Jest to równanie okręgu o środku S = (		; 0) i r =
	3		3

Eta: Ooo Janek urwał się z.......

Michał: jeszcze raz dziękuję