GEOMETRIA ANALITYCZNA zosia: Proszę o pomoc w zadaniu:Wierzchołek C trójkąta ABC jest punktem przecięcia się prostych o równaniach y=x+2 i y=−2x+14,a wierzchołki A i B są punktami przecięcia się tych prostych z osią OX.Oblicz pole i obwód trójkąta ABC

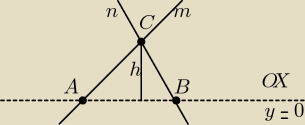
xor: m: y = x+2 n: 2x+14 C: x+2=2x+14 −x=12 x=−12 C=(−12,−10) A: 0=x+2 x=−2 A=(−2,0) B: 0=2x+14 x=−7 B=(−7,0) Wystarczy teraz obliczyć |AB| + |BC| + |CA| i odległość punktu C od prostej y=0 (czyli h na rysunku).

	|AB| * h
I pole
	2

kaz: y=x+2 y=−2x+14 rozwiązując ten układ równań otrzymujemy C(4,6) punkt A jest rozwiązaniem układu y=x+2 y=0 A(−2,0) punkt B y=−2x+14 y=0 B(7,0)

	1		9*6
P=		IABI*h=		=27
	2		2

kaz: xor coś Ci nie wyszło

marta: kaz a moze mi pomozesz? bede bardzo wdzieczna

zosia: dziękuję