Oblicz promień okręgu opisanego na trapezie równoramiennym o podstawach długości mielony: Oblicz promień okręgu opisanego na trapezie równoramiennym o podstawach długości 20 i 52 oraz wysokości 12.

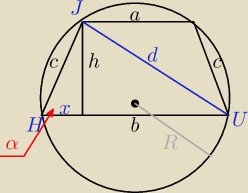
x: a=20 b=52 h=12

	b−a
x=		=16
	2

c=√h²+x²=20 d=√h²+(b−x)²=12√10

	12
sinα=
	20

	d
R=		≈11,38
	2sinα

.... ? ? ? ..... profit skorzystałem z tego, że na ΔHUJ można opisać taki sam okrąg, nie wiem czy słusznie, bo północ

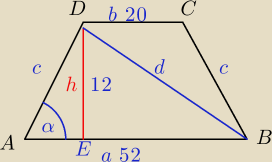
Mila: |AE|=(52−20):2=32:2=16 c²=16²+12² c²=256+144 c=20

	12		3
sinα=		=
	20		5

cosα=√1−(9/25)

	4
cosα=
	5

W ΔDAB:

	4
d2=202+522−2*20*52*
	5

d²=400+2704−32*52 d²=3104−1664=1440 d=√144*10=12√10 okrąg opisany na ΔABD jest jesdnocześnie okręgiem opisanym na trapezie ABCD. Z tw. sinusów:

d
	=2R
sinα

12√10
	=2R
35

R=10√10 Sprawdź rachunki, albo odpowiedź w książce.

x: tfu R≈31,62, źle w liczydło wklepałem