GEOMETRIA ANALITYCZNA zosia: Proszę o pomoc w zadaniu:Wierzchołek C trójkąta ABC jest punktem przecięcia się prostych o równaniach y=x+2 i y=−2x+14,a wierzchołki A i B są punktami przecięcia się tych prostych z osią OX.Oblicz pole i obwód trójkąta ABC

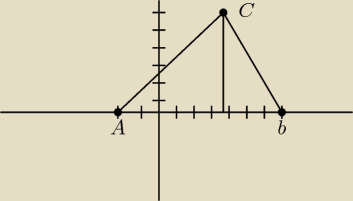
Godzio: wyznaczamy punkt C y=x+2 , y=−2x+14 x+2=−2x+14 3x=12 x=4 y=6 C(4,6) punkt A: y=x+2 (punkt przecięcia z OX −> x=..., y=0) 0=x+2 x=−2 A(−2,0) punkt B: y=−2x+14 0=−2x+14 −14=−2x x=7 B(7,0) wysokość ma długość 6 liczymy długość odcinka AB : |AB|=√(−2−7)²+(0−0)²=√81=9 długość BC: √(4−7)²+ (6−0)²=√9+36=√45=3√5 dł. CA: √(4+2)²+ (6−0)² = √72=6√2

	9*6
P=		=27
	2

l=3√5+6√2+9=3(√5+2√2+3)

Godzio: wysokośc na rysunku powinna padać na punkt (4,0) jak coś