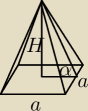Wyznacz objętość ostrosłupa prawidłowego czworokątnego Ann: Wyznacz objętość ostrosłupa prawidłowego czworokątnego, którego pole powierzchni całkowitej jest równe S, a ściany boczne są nachylone do płaszczyzny podstawy pod kątem α.

Ann: ?

prosta: h − wysokość ściany bocznej

	a		(S −a2)2
(		)2+H2=h2 i a2+2ah=S ⇒ 2ah=S−a2 ⇒ h2=
	2		4a2

a 2		(S −a2)2
	+H2=
4		4a2

	(S −a2)2−a4		S2−2a2S+a4−a4
H2=		⇒ H2=
	4a2		4a2

	√S2−2a2S		a2	√S2−2a2S		a√S2−2a2S
H=		V=			=
	2a		3	2a		6