Bryły obrotowe- objętość rak: w trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki których długości pozostają w stosunku 1:3. Oblicz stosunek objętości brył powstałych w wyniku obrotu tego trójkąta wokół dłuższej i krótszej przyprostokątnej.

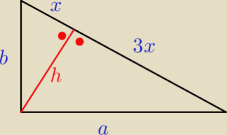
Janek191:: c = x + 3 x = 4 x

	1
V1 =		π b2*a
	3

	1
V2 =		π a2*b
	3

więc

V1		b2*a		b
	=		=
V2		a2*b		a

oraz h² = 3 x² h = √3 x więc

h		3x
	=
b		a

√3 x		3x		b		√3
	=		⇒		=
b		a		a		3

V1		√3
	=
V2		3

==================

pigor: ..., albo od momentu V₁ : V₂ = b : a ; b²=x*4x i a²=3x*4x ⇔ b²=4x² i a²= 12x² ⇒ ⇒ b= 2x i a= 2√3x ⇒ ^b_a = ¹_√3= ¹₃√3 ...