środek masy kyrtap: Ktoś pomoże z analizy wektorowej z wytłumaczeniem przykładu? http://prntscr.com/6cslnc jak znaleźli ten środek symetrii i przedstawili tę cykloidę

Qulka: a może być najpierw wersja punktowa będzie bez całek

Qulka: czy tak ogólnie to wiesz jak się wyznacza środek symetrii tylko pytasz o coś trudniejszego

kyrtap: po prostu nie rozumiem tego zadania znam wzór środka masy ale jak tu znaleźć ten x środka masy to nie wiem

Qulka: tak jak napisali..oś symetrii skoro zaczyna się na 0 i kończy na 2πa to środek

0+2πa
	= πa
2

Qulka: gdyby nie była symetryczna to też całki

kyrtap: dziwne to

Qulka: miłe że tak można sobie ułatwić najlepiej jest jak jest kółeczko

Qulka: o ile jest jednorodne

kyrtap: w ogóle w skoczylasie same wzory są nic nie piszą o jednorodnym czymś mało też jest parametryzacji jeśli coś parametryzujemy tylko częściowo

Qulka: ja mam w Skoczylasie oddzielnie wzory a oddzielnie zadanka weź sobie Krysickiego

kyrtap: ja też lepszy jest?

Qulka: na nim się uczyłam więc dla mnie na pewno lepszy ma od razu na przykładach wyjaśniane wzorki więc łatwiej je zrozumieć

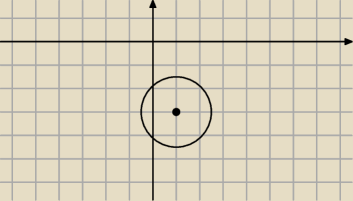
kyrtap: wzory kminie ale przykładowo mam takie zadanie że mam napisać parametryzacje łuków dla każdego z kierunku przebiegu i tak podpunkt: część okręgu x² − 2x + y² + 6y + 8 = 0 leżąca w IV ćwiartce jak to zrobić ? wiem że muszę odczytać współrzędne środka okręgu i promień

Qulka:

kyrtap: no widzę że część okręgu będzie oderwana

Qulka: niom zapomniałam o Tobie i zajęłam się algorytmami idę szukać krysickiego

kyrtap: przy okazji napisz w jaki sposób sparametryzować ten okrąg

Qulka: przerobić niewiadome na kąt

kyrtap: w sensie?

Qulka: może najpierw takie inne równe kółeczko zróbmy

kyrtap: ja nie czaję tego bo w skoczylasie jest wzór podany na cały okrąg

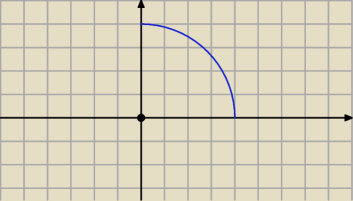
Qulka: np zamiast pisać I ćwiartka koła x²+y²= 4 to masz parametr α i x= cosα y=cosβ r=4 i dla α∊<0;90°> x=rcosα y=rsinα

Qulka: tu masz zwór na ćwiartkę

kyrtap: no rozumiem a w przypadku naszym jak znaleźć ten kąt ?

Qulka: od −135 do 135

Qulka: czyli Twój przykład to dla α∊<−135°;135°> x=√2cosα+1 y=√2sinα−3

kyrtap: Qulka ale jak te kąty liczyć i czemu akurat od −135 do 135 możesz to wytłumaczyć

kyrtap:

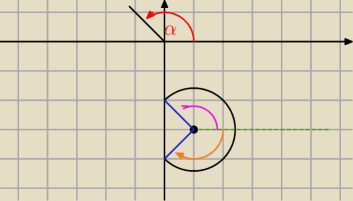
Qulka: tak jak kąty między prostą a osią x , tak tu mierzysz od równoległej do osi w górę (+) i w dół (−)