tw. cosinusów
Adrian:
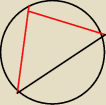
Z tego samego punktu okręgu o promieniu r poprowadzono dwie cięciwy o długościach r
√3 i r
√2√3. Oblicz miare kiąta między tymi cięciwami, jeśli wiesz, że sin 15 =
√2−√32
Czy czarny odcinek równa się 2r ?
jezeli nie to jaki rysunek należy tu zrobić i jak zastosować twierdzenie cosinusów/sinusów by
to zadanie rozwiązać ?
4 mar 21:20
Mila:
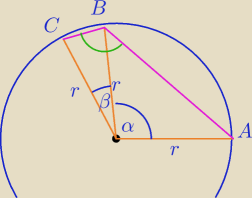
|AB|=r
√3
|BC|=(2
√3)
12 =
4√12 nie wiem, czy dobrze odczytałam .
Podaj odpowiedź, jeśli masz podaną.
4 mar 21:40
Adrian: 45 lub 105
4 mar 22:01
Mila:
Poprawię rysunek.
Licz na razie wg tego .
4 mar 22:07
Mila:
Adrian wydaje mi się ,że pod jednym pierwiastkiem powinno być inaczej
druga cięciwa :
r*√2−√3
4 mar 22:39
Mila:
AB=r√3
BC=r√2−√3
α=1200
β=30o
∡CBA=30+75=105
II wariant
Punkt C z prawej
∡ACB=75−30=45o.
4 mar 22:48
Adrian: Skąd wzięłaś, ze α=120 ?
4 mar 23:06
Mila:
Można obliczyć na kilka sposobów.
Np. z tw. cosinusów, albo narysować wysokość do boku AB
Wtedy :
α=120
wΔCBO:
[(
√2−√3)]
2*r
2=r
2+r
2−2*r*r cosβ /:r
2⇔
2−
√3=2−2cosβ
β=30
o
Mam narysować jeszcze raz, abyś widział drugi wariant?
4 mar 23:20
Adrian: Tak tylko o rysunek poproszę.
Zrobiłem to w nieco inny sposób :
z tw. cosinusów i jakoś wyszło jednak sporo sie naliczyłem
4 mar 23:29
Mila:
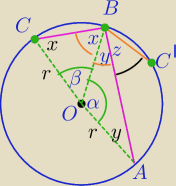
Odcinka OC' nie rysuję , aby nie zaciemniac obrazu.
β=30
o
x=(180−30):2
x=75
o
Kąt α z tw. cosinusów :
(r
√3)
2=r
2+r
2−2r
2 cosα
3r
2=2r
2−2r
2*cosα /:r
2
3=2−2 cosα
1=−2cosα
===================
y=(180−120):2=30
o
∡ABC=x+y=75+30=105
o
lub z+y=75
o
stąd
∡ABC'=z−y=75
o−30
o=45
o
5 mar 00:07
Adrian: skąd wiesz, że katy x są równe ?
5 mar 00:20
Mila:
Bokami są promienie okręgu, zatem trójkąty COB i AOB są równoramienne.
5 mar 00:21
Adrian: W zadaniu trzeba obliczyć kat pomiędzy cięciwami AB i CD to dlaczego ten kat z ?
Czemu tam ?
5 mar 00:26
Mila:
Bo ktoś może narysować cięciwę BC z lewej strony AB, a ktoś inny z prawej strony cięciwy AB.
Należy rozważyć obie sytuacje.
Dobranoc

5 mar 00:32
Adrian: aaa, dziękuję

Dobranoc

5 mar 00:35
 Z tego samego punktu okręgu o promieniu r poprowadzono dwie cięciwy o długościach r √3 i r
√2√3. Oblicz miare kiąta między tymi cięciwami, jeśli wiesz, że sin 15 = √2−√32
Czy czarny odcinek równa się 2r ?
jezeli nie to jaki rysunek należy tu zrobić i jak zastosować twierdzenie cosinusów/sinusów by
to zadanie rozwiązać ?
Z tego samego punktu okręgu o promieniu r poprowadzono dwie cięciwy o długościach r √3 i r
√2√3. Oblicz miare kiąta między tymi cięciwami, jeśli wiesz, że sin 15 = √2−√32
Czy czarny odcinek równa się 2r ?
jezeli nie to jaki rysunek należy tu zrobić i jak zastosować twierdzenie cosinusów/sinusów by
to zadanie rozwiązać ?
 |AB|=r√3
|BC|=(2√3)12 =4√12 nie wiem, czy dobrze odczytałam .
Podaj odpowiedź, jeśli masz podaną.
|AB|=r√3
|BC|=(2√3)12 =4√12 nie wiem, czy dobrze odczytałam .
Podaj odpowiedź, jeśli masz podaną.
 Odcinka OC' nie rysuję , aby nie zaciemniac obrazu.
β=30o
x=(180−30):2
x=75o
Kąt α z tw. cosinusów :
(r√3)2=r2+r2−2r2 cosα
3r2=2r2−2r2*cosα /:r2
3=2−2 cosα
1=−2cosα
Odcinka OC' nie rysuję , aby nie zaciemniac obrazu.
β=30o
x=(180−30):2
x=75o
Kąt α z tw. cosinusów :
(r√3)2=r2+r2−2r2 cosα
3r2=2r2−2r2*cosα /:r2
3=2−2 cosα
1=−2cosα

 Dobranoc
Dobranoc 