Geometria analityczna Wioletta : Proszę o sprawdzenie czy dobrze rozwiązałam zadanie. Jutro mam sprawdzian z geometrii analitycznej ale nie wiem czy dobrze zrobiłam zadanie, które ma się jutro pojawić. Treść jest następująca: Napisz równanie odcinka AB, gdzie A=(−4,3) B=(5,−1) Najpierw wyznaczyłam długość odcinka /AB/= √97 Następnie współrzędne środka S=(0,5 ; 1) i to z czym mam wątpliwość (od razu napiszę moje rozwiązanie): y=ax+b 3=−4x+b −1=5x−b −−−−−−−−−−−−− 4=−9x / : (−9) − ⁷₉=x 3=−4*( −⁴₉ ) +b ¹¹₉ =b więc: y= −⁴₉ x + ¹¹₉

ax: ... to może zacznij od poprawnego zapisania treści zadania

Wioletta : Tylko treść brzy tak: Napisz równanie odcinka AB, gdzie A=(−4,3) B=(5,−1) i żadnych innych informacji nie ma.

ax: ... to masz problem. Nie rozumiesz nawet jaki.

5-latek: Ja podejrzewam ze to ma byc > napisz rownanie symetralnej odccinka AB

ax: Pewnie w treści jest: "napisz równanie symetralnej odcinka ... ]]

Wioletta : To najwyraźniej musiałam nie usłyszeć kluczowego słowa. I czy to rozwiązanie, które wykonałam jest poprawne?

prosta: zapis jest nieprawidłowy....w układzie powinny wystąpić niewiadome a i b ...równania też z błędami

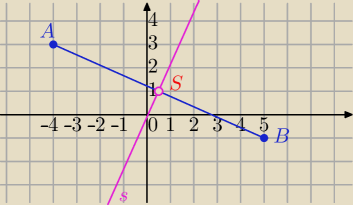
Mila: Symetralna AB, gdzie : A=(−4,3) B=(5,−1) I sposób: 1) równanie prostej AB: y=ax+b 3=−4a+b i −1=5a+b ======== odejmuję stronami:

	−4
4=−9a⇔a=
	9

	4
y=−		x+b , nie liczę b , bo potrzebny jest wsp. kierunkowy.
	9

Symetralna jest prostopadła do AB i przechodzi przez środek AB.

	−4+5		3−1		1
S=(		,		)=(		,1)
	2		2		2

	−4		9
y=ax+b , a*		=−1⇔a=
	9		4

	9		9		1
s: y=		x+b i S∊symetralnej⇔1=		*		+b
	4		4		2

	9		1
1=		+b⇔b=−
	8		8

	9		1
s: y=		x−
	4		8

II sposób: Symetralna jest zbiorem punktów jednakowo odległych od końców odcinka. Niech P(x,y) będzie punktem należącym do symetralnej AB. √(x+4)²+(y−3)²=√(x−5)²+(y+1)² /² (x+4)²+(y−3)²=(x−5)²+(y+1)² ⇔ x²+8x+16+y²−6y+9=x²−10x+25+y²+2y+1⇔ 8x+16−6y+9=−10x+25+2y+1⇔ −8y=−18x+1 /:(−8)

	9		1
y=		−
	4		8

===========

Mila:

	9		1
y=		x−
	4		8

PW: Polecenie "napisz równanie odcinka" też jest sensowne. Jeżeli A = (− 4, 3) i B = (5, − 1), to P = (x, y)∊AB ⇔ |AP| + |PB| = |AB| Można się bawić z takim równaniem, można należenie do odcinka zapisać w postaci wektorowej: AP^→ = t· AB^→, t∊[0, 1] [x +4, y−3] = t·[5+4, −1−3] [x+4, y −3] = t·[9, −4] (1) x+4 = 9t i y − 3 = −4t, t∊[0, 1]

	⎧	x = 9t −4
	⎩	y =−4t+3, t∊[0, 1]	.

Jest to równanie parametryczne odcinka; z postaci (1) można też wywnioskować jak wygląda "równanie odcinka w postaci kierunkowej", czyli równanie jak dla prostej prostej z odpowiednim ograniczeniem dla x.

Mila: Straciła zainteresowanie.

PW: No i było dzisiaj na sprawdzianie równanie odcinka?