wartość parametru p, funkcja marvol: Dla jakiej wartości parametru p funkcja f(x)=(2p²+p)^x jest funkcją wykładniczą malejącą?

marvol: niech mi ktoś pomoże

Qulka: gdy 0< 2p²+p <1

pigor: ..., funkcja wykładnicza f(x)=a^x jest malejąca (rosnąca) ⇔ 0<a<1 (a>1), zatem tu np. tak : f(x)=(2p²+p)^x ⇒ 0< 2p²+p <1 ⇔ 0< 2p²+p i 2p²+p< 1 ⇔ ⇔ 2p²+p >0 i 2p²+p−1< 0 ⇔ 2p(p+¹₂) >0 i 2p²+2p −p−1< 0 ⇔ ⇔ (*) (p< −¹₂ v p>0) i 2p(p+1)−1(p+1)< 0 ⇒ 2(p+1)(p−¹₂)< 0 ⇔ ⇔ −1< p< ¹₂, stąd i z (*) ⇔ p∊(−1;−¹₂) U (0;¹₂) . ...

marvol: Dziękuje! Spróbuje to jakoś zrozumieć, mam nadzieję że się uda

marvol: p< −12 v p>0 dlaczego jest p<−1/2 ? a nie powinno być p>−1/2?

pigor: ..., narysuj sobie parabolę y= p(p+¹₂) (y=x(x+¹₂) i odczytaj na osi Op (Ox) dla jakich p (x−ów) y=f(p) >0 (dodatnie), czyli ramiona (gałęzie) paraboli są nad osią Op .

marvol: :Już rozumiem A mógł/abyś mi jeszcze podpowiedzieć jak rozwiązać równanie 1/2sin5/4π : sinπ/4=k ?

pigor: ..., np. tak :

12sin54π		12sin(π+π4)
	= k ⇔		= k ⇔
sinπ4		sinπ4

	12(−sinπ4)
⇔		= k ⇔ 12*(−1}=k ⇔ k= − 12. ...
	sinπ4

Jacek: 2^−x>2^x−1 2^−x jest funkcją malejącą 2^x−1 jest funkcją rosnącą , a jednak porównujemy wykładniki potęg bez zmiany znaku nierówności i wychodzi prawidłowo

	1
x<
	2

Widzę, że to działa, ale ciekawi dlaczego jak porównujemy a^x jest malejąca (rosnąca) ⇔ 0<a<1 (a>1), to dla odwrócenia znaku ma znaczenie czy jest funkcja są rosnąca czy malejąca. Ale w podanym przez mnie przypadku jedna funkcja jest malejąca, druga rosnąca, znaku nie odwracam i wychodzi poprawnie.

Qulka: znak zmieniasz tylko jak podstawa jest ułamkiem, bo minus został w wykładniku i uwzględniasz go w dalszych obliczeniach

Qulka: a zmieniasz bo (1/2)³ < (1/2)² ale już 3 > 2

Qulka: poza tym wyliczasz konkretne iksy więc jeśli 2 do jakiejś liczby > 2 do innej to nadal tamta > niż ta inna bo funkcja 2^x jako taka jest rosnąca

Qulka: może lepiej jeśli 2^a >2^b to nadal a>b nawet jak a jest akurat jakąś liczbą ujemną

Jacek: Czyli zasadniczo po co wspominać czy funkcja wykładnicza o podstawie a jest rosnąca czy malejąca, kryterium jest wartość podstawy, a jak wykładnik będzie "sterował" (rosnąco czy malejąco) wartościami funkcji nie ma znaczenia?

Qulka: kryterium jest wartość podstawy, a bierze się to stąd że taka jest właściwość funkcji

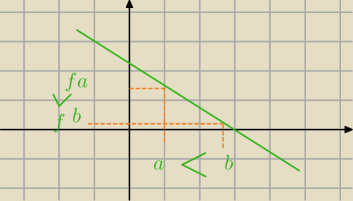
Qulka: malejąca ma taką właściwość f(a) > f(b) ale a <b obojętnie czy wykładnicza czy logarytmiczna czy inna

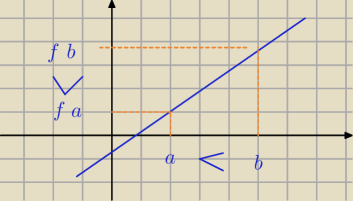
Qulka: rosnąca ma taką właściwość f(a) < f(b) i a<b

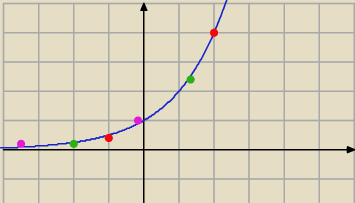
Qulka: 2^x i nadal 2⁻¹ <2² to −1<2 mimo że te szukany wykładnik (oznaczany jako x) jest ujemny również 2⁻³ <2⁻²

Jacek: Czyli powinienem zapisać ogólniej: g(f(x))=a^f(x) I teraz: g(f₁(x))>g(f₂(x)) a^f₁(x)>a^f₂(x) to gdy a>1 f₁(x)>f₂(x) to gdy a<1 f₁(x)<f₂(x)

Qulka: Tak