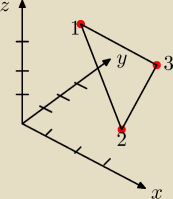
Trójkąt w przestrzeni, wektory. Dawid: Znajdź kąty w trójkącie o wierzchołkach P₁(1,2,3) P₂(3,1,1) P₃=(3,3,3) Z czego skorzystać i jak obliczyć? Dziękuje.

Dawid: ?

bezendu: 1.Obliczam wektor BA^→ i BC^→ BA^→=[−2,1,2] BC^→=[0,2,2] 2.Iloczyn skalarny wektorów BA i BC BA*BC=2+2=4 Długość wektora BA i BC |BA|=√(−2)²+1²+2²=3 |BC|=√2²+2²=2√2

	4
cos(∡BA, BC)=
	3*2√2

	√2
cos(∡BA, BC)=
	3

Resztę analogicznie

AS: A tw.cosinusów,znasz,kąt między wektorami i wiele innych metod. Czy musisz o wszystko się pytać? Znajdowanie to też pewna satysfakcja.

Dawid: Czy wyjdą kąty 35.26^o,114,09^o,30,65^o ?

Dawid: są jakieś programy którymi można sprawdzić ?

Dawid: P₁P₂^→

Dawid: P1P2^→[1,−1,−1] P1P3^→[1,1,1] P1P2^→*P1P3^→=−1 |P1P2^→|=√3 |P1P3^→|=√3

	−1
cos(∡ P1P2→, P1P3→)=		=114,09o
	√6

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− P2P1^→[−1,1,1] P2P3^→[0,2,2] P2P1^→*P2P3^→=4 |P2P1^→|=√3 |P2P3^→|=2√2

	4		√6
cos(∡ P2P1→, P2P3→)=		=		=35.26o
	2√2*√3		3

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Zatem: ∡(P3P1^→,P3P2^→)=(180−35.26−114.09)=30.36^o Dobbrze?

Dawid: Bo coś mi nie wychodzi. Jak policzę P3P2^→[0,−2,−2] P3P1^→[−1,−1,−1] P3P2^→*P3P1^→=4 |P3P2^→|=2√2 |P3P1^→|=√3 i wyjdzie kąt 35.26^o

Dawid: ?