pomocy!!!! Akson: W prostokącie o wymiarach 9 cm x 7 cm umieszczono mniejszy prostokąt tak, że jedna z jego przekątnych łączy środki krótszych boków większego prostokąta, a dwa pozostałe wierzchołki małego leżą na dłuższych bokach dużego. Oblicz obwód mniejszego prostokąta.

daras: narysuj to sam zobaczysz jakie to proste

Akson: naryzowałem i nie widzę nic!

Akson: nie widzę !

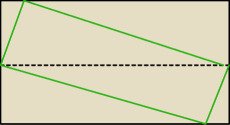
J: Mniej więcej coś takiego

Akson: no wiem i?

J: oznacz w zielonym : x krótszy bok , y dłuższy bok

	3.5		x
masz: x2 + y2 = 92 oraz		=
	y		9

Jacek:

	3.5
A z czego ta proporcja wynika, bo np.		to jest sin konkretnego kąta, ale nie widzę
	y

podobnego kąta którego sin byłby x/9?

Jacek: sorry cos nie sin

Qulka: (x+y)²−2xy =81 2xy=7•9 (x+y)² = 81−63 =18 x+y = 3√2 obwód = 6√2

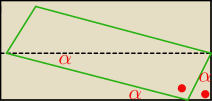
J: z podobieństwa trójkątów .. .w dolnej połowie dużego prostąkata mamy dwa podobne trójkąty prostokątne , bo mają takie same kąty: jeden to: dwie zielone przyprostokatne i przerywana przeciwprostokatna drugi to: dwie czarne przyprostokatne i zielona przeciwprostokatna

Qulka:

J: Własnie rysunek Qualki pokazuje równe kąty

Jacek: Dzięki.

Akson: no ale ja nie wiem co dalej

J: Przecież to już koniec zadania .. patrz: 11:36

Akson: a co to jest x y?

J: patrz 11:13

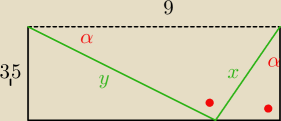
Qulka: narysowałam tylko pół żeby było widać x,y boki małego Twierdzenie Pitagorasa x²+y²=9²

	3,5		x
trójkąty podobne		=
	y		9

ułamki mnożymy na krzyż 2xy=7•9 =63 x²+y² = (x+y)² −2xy wzór skróconego mnożenia x²+y²=9² (x+y)²−2xy =81 (x+y)² = 81−63 =18 x+y = 3√2 obwód = 2•(x+y) = 6√2

Qulka: to 3.5 powinnam narysować z drugiej strony

Akson: a tam jak było (x+y)² −2xy=81 to ty odjęłaś 63 a nie powinnaś dodać?

Akson: wtedy wyszłoby x+y=12

Qulka: powinnam dodać... brawo

Akson: w końcu sobie z czymś poradziłem

Qulka: