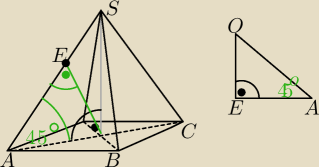
Wyznacz odległość spodka od.. Frytka: Objętość ostrosłupa prawidłowego czworokątnego wynosi ^4√2₃ dm³. Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy 45 stopni. Wyznacz odległość wysokości spodka od: a) krawędzi bocznej b)ściany bocznej ostrosłupa Zaczęłam podpunkt a) i wiem, że : |AO|=¹₂d d=a√2 ¹₂d=^a√2₂ Pp=a² V=¹₃a²H Dalej nie wiem co zrobić , proszę o pomoc.

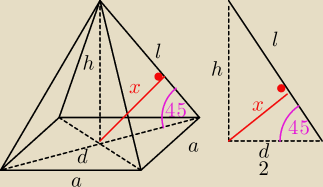dero2005: nie wysokości spodka tylko spodka wysokości a)

a2h		4√2
	=
3		3

h
	= tg45o = 1
d   2

	d		√2
h =		=
	2		2

a2		a√2		4√2
	*		=
3		2		3

a = 2 d = a√2 = 2√2

x		√2
	= sin 45o =
d   2		2

x = 1

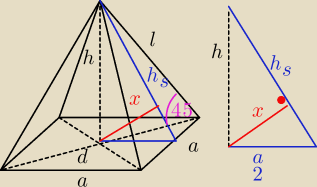dero2005: b)

a2h		4√2
	=
3		3

d		a√2
	=
2		2

h
	= tg45o = 1
d   2

	d		a√2
h =		=
	2		2

a2		a√2		4√2
	*		=
3		2		3

a = 2

d   2		√2
	= cos45o =
l		2

l = a

	a√3
hs = √l2 − (a2)2 =		= √3
	2

	a
x*hs =		*h
	2

x =

Frytka: A tak przepraszam. Podpunkt b) nie wiem czy dobrze ale wyszło mi że x= ^√6₃ Bardzo dziękuję za pomoc w rozwiązaniu

Robert: @daro Skąd w podpunkcie a wzięło się h = d/2 = √2 /2 ? Szczególnie to √2 /2