Pole ograniczone
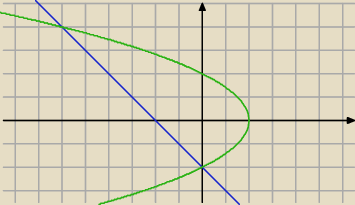
Magik: Obliczyć pole obszaru D ograniczonego prostą x+y=−2 oraz y
2=4−2x
Zrobiłem rysunek i wyszło mi coś takiego:
D
OY:
−2≤y≤4
Więc:
| | 1 | |
|D|=∫−24(− |
| y2+y+2)dy gdzie wynik wyszedł mi .....=6 . |
| | 2 | |
Nie wiem czy to prawidłowy wynik,bo jeśli patrze na rysunek to te pole ma więcej jednostek niż
6 .Może ktoś skomentować?
3 mar 14:16
Qulka:
3 mar 14:18
Magik: Tak właśnie narysowałem i konfrontując z moim wynikiem chyba coś jest źle

3 mar 14:23
Qulka: chyba te pod osią się odejmują

3 mar 14:24
Qulka: a nie.. tobyś miał na minusie

sprawdze rachunki Twoje najpierw

3 mar 14:25
Magik: No raczej nie

Tak myślę...
3 mar 14:25
Qulka: a gdzie zgubiłeś 4

3 mar 14:26
Magik: Może niewyraźnie zapisałem (nie wiem jak dodaje się ale to granice całkowania

3 mar 14:26
Qulka: −y2/2+y+6
3 mar 14:27
Qulka: we wzorze Ci zginęła
3 mar 14:28
Magik: Nie rozumiem Cię teraz

3 mar 14:31
J:
| | 1 | |
policz to jako ... ∫∫ [](x + 2) − ( |
| x2 − 2)]dxdy w granicach: |
| | 2 | |
| | 1 | |
− 2 ≤ x ≤ 6 |
| x2 − 2 ≤ y ≤ x + 2 |
| | 2 | |
3 mar 14:38
J:
literówka: − 2 ≤ x ≤ 4
3 mar 14:38
Qulka: miałeś policzyć całkę z tego co napisałam a nie z tego co policzyłeś
3 mar 14:40
Magik: Ale to nie ja pisałem

Znalazłem u siebie błąd i musze obliczy taką całkę
| | 1 | |
∫(− |
| y2+y+4)dy w wcześniejszych granicach jednak i tak mi te pole większe nie wychodzi.. |
| | 2 | |
3 mar 14:49
Magik: Qulka obliczyłem Twoją całkę (nie wiem skąd 6) wyszło 30 więc niemożliwe

3 mar 14:53
Qulka: bo (2−y
2/2) − (−y−2) to −y
2/2+y +4

Ty ją zgubiłeś a ja zapomniałam podzielić

3 mar 14:57
Magik: | | −1 | |
No tak,więc fuzja "mojej" i "Twojej" całki to właśnie ∫( |
| y2+y+4 )dy i wyszło mi |
| | 2 | |
28−14=14 ?
3 mar 14:58
Magik: | | 1 | | 1 | |
=− |
| y3+ |
| y 2+4y w granicach od −2 do 4  więc tak mi wyszło.... |
| | 6 | | 2 | |
=−12+20−2+8=28−14
3 mar 15:01
Qulka: wygląda rozsądnie

3 mar 15:03
Magik: W Wolphramie wychodzi 18... :\
3 mar 15:06
J:
masz błąd w obliczeniach .. .wynik to 18

3 mar 15:08
Magik: No dzięki J ,możesz podpowiedzieć gdzie?

3 mar 15:09
J:
| | 64 | | 8 | |
= − |
| + 8 + 16 − |
| − 2 + 8 = − 12 + 30 = 18 |
| | 6 | | 6 | |
3 mar 15:10
Magik: Dzięki.... w tabliczce mnożenia sie pomyliłem

i zadanie źle...

3 mar 15:11
Magik: a jak już jesteśmy w tym temacie :
To pole ograniczone :
y=x2;y=2x2 oraz prosta y=8 i w nawiasie podane jest (x≥0) czyli mam brać tylko obszar na
prawo od x=0?
W tym wypadku trzeba podzielić na D1 w 0≤x≤2√2 i x2≤y≤2x2 itd.? Analogicznie z drugim
polem?
3 mar 15:14
Qulka: mi z tego co napisałeś też wychodzi 18

3 mar 15:15
Magik: Okej ,dzięki Qulka i J, spojrzycie na kolejne?
3 mar 15:20
J:
| | 1 | |
P = D1 − D2 , gdzie: D1 = ∫ (8 − |
| )dx w granicach: <0,4> |
| | x2 | |
D
2 = ∫ (8 − x
2)dx w granicach : <0,2
√2>
3 mar 15:22
J:
| | 1 | |
upss... D1 = ∫ (8 − |
| x2)dx |
| | 2 | |
3 mar 15:23
Qulka:
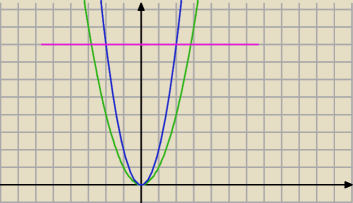
tu na dwa kawałki (dwie całki )
od 0 do 2 z 2x
2−x
2 + od 2 do 2
√2 z 8−x
2
3 mar 15:24
Magik: J a mogę takie coś zrobić:
D
1:
0≤x≤2
x
2≤y≤2x
2
d
2:
2≤x≤2
√2
8≤y≤x
2
Tak wychodzi z mojego rysunku

Dlaczego u Ciebie jest różnica i skąd ten przedział <0;4> ?
3 mar 15:25
Magik: Qulka właśnie to tak rozkminiłem

Super!
3 mar 15:26
J:
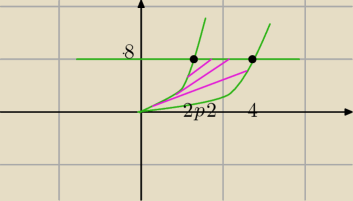
3 mar 15:27
Magik: Qulka nie powinno być x2−8 ?
3 mar 15:28
J:
Różnica pól

obszar zakreskowany
3 mar 15:28
Qulka: od górnej odejmujesz dolną góra to 8 dół to x2
3 mar 15:29
Magik: J mi wyszło tak jak Qulkce ,że rozbijam na x od <0;2> potem od <2;2√2>
3 mar 15:29
J:
Liczymy to samo pole , tylko innymi metodami

3 mar 15:30
J:
Wy dodajecie pola , a ja odejmuję

3 mar 15:31
Magik: Jotek

Nie rozumiem ,jakie pole odejmujesz od którego

Uporządkuje swoja metodę

D
1:
0≤x≤2
x
2≤y≤2x
2
D
2:
2≤x≤2√2
x
2≤y≤8
| | 8 | |
D1=∫x2 dx w granicach <0;2> więc D1= |
| |
| | 3 | |
| | 1 | | 16√2 | | 8 | |
D2=∫(8−x2)dx=8x− |
| x2 w granicach <2;2√2> więc D2=16√2− |
| −16+ |
| |
| | 3 | | 3 | | 3 | |
Więc: P=D
1+D
2=...
3 mar 15:34
J:
| | 1 | |
upss ... wycofuje swoje posty ... .ja wziąłem drugą funkcję: y = |
| x2 , a nie: y = 2x2 |
| | 2 | |

3 mar 15:35
Qulka: Magik

OKI
3 mar 15:37
Magik: Właśnie

Coś mi sie nie zgadzało z tymi granicami całkowania

Moje uporządkowanie jest dobre?
3 mar 15:37
Qulka: tak, to uporządowanie jest OK
3 mar 15:42
J:
tak ... i można to robić sumą pól, albo róznicą:
P =D1 − D2 , gdzie D1 = ∫(8 − x2)dx w <0,2√2>
D2 = ∫(8 − 2x2)dx w <0,2>
3 mar 15:43
Magik: Fakt, to logiczne przecież ,gupi ja

3 mar 16:04
Magik: Z kolei jeśli mam : y=arctgx ,y=arcctgx i oś OY to dzele też na:
D
1:
0≤x≤1
0≤y≤arctgx
Tak wychodzi mi z rysunku
D
2:
1≤x≤
∞
0≤y≤arcctgx
P=D
1+D
2 
A jakbym chciał względem OY to bym wział :
Ale tu nie można stwierdzić która funkcja ogranicza?

Więc odpada liczenie względem OY?
3 mar 16:14
Qulka:
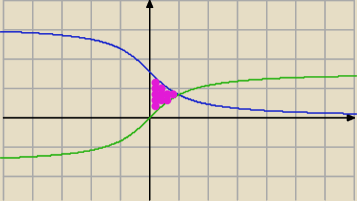
czemu ty się tak upierasz przy tym y
całka od 0 do 1 z arcctg(x) − arctg(x)
3 mar 16:44
Qulka: dx oczywiście

3 mar 16:45
Magik: y=0 to to inny wykres

3 mar 16:49
Magik: Dobra pomyliłem

3 mar 16:56
Qulka: 
3 mar 16:58
Magik: No to obliczyłem te dwie całki 2 razy przez części i wyszedłem na coś takiego:
| | 1 | | 1 | |
P=∫(arcctgx−atctgx)dx=xarcctgx+ |
| ln|x2+1|−xarctgx+ |
| ln|x2+1| czyli będzie |
| | 2 | | 2 | |
| | 1 | |
=xarcctgx−xarctgx+ |
| ln|x2+1| w granicach <0;1> |
| | 4 | |
?
3 mar 17:12
Magik: halo,halo

3 mar 18:07
3 mar 18:17
Qulka: ale jak dla mnie 1/2 +1/2 = 1
3 mar 18:19
Magik: | | 1 | | 1 | | 1 | |
lol,lol, jaki błąd u mnie  |
| + |
| = |
|  Ja to jestem....szalony  ale tak |
| | 2 | | 2 | | 4 | |
jest,jak trudniejsze rzeczy to na takich łatwych człowiek się wykłada...
Te całki jednak myślę,że dobrze obliczyłem

3 mar 18:26
Qulka: całki OK

3 mar 21:41
Magik: Ale jak dalej ,zrobic oznaczoną bo kosmos mi wychodzi po podstawieniu...
4 mar 17:41
Magik: halo,halo?

5 mar 14:39
Qulka: Napisz jaki bo przy kompie będę dopiero nocą
5 mar 15:20
Qulka: wolframa mówi że wynik to ln2

5 mar 22:37
Qulka: no przecież
1•arcctg1 −1•arctg1+ln|1+1| − ( 0arcctg0 −0 arctg0+ln1) = π/4 − π/4 + ln2 −(0−0+0)= ln2
5 mar 23:52



 sprawdze rachunki Twoje najpierw
sprawdze rachunki Twoje najpierw 
 Tak myślę...
Tak myślę...



 Znalazłem u siebie błąd i musze obliczy taką całkę
Znalazłem u siebie błąd i musze obliczy taką całkę

 Ty ją zgubiłeś a ja zapomniałam podzielić
Ty ją zgubiłeś a ja zapomniałam podzielić 
 więc tak mi wyszło....
więc tak mi wyszło....


 i zadanie źle...
i zadanie źle... 

 tu na dwa kawałki (dwie całki )
od 0 do 2 z 2x2−x2 + od 2 do 2√2 z 8−x2
tu na dwa kawałki (dwie całki )
od 0 do 2 z 2x2−x2 + od 2 do 2√2 z 8−x2
 Dlaczego u Ciebie jest różnica i skąd ten przedział <0;4> ?
Dlaczego u Ciebie jest różnica i skąd ten przedział <0;4> ?
 Super!
Super!

 obszar zakreskowany
obszar zakreskowany


 Nie rozumiem ,jakie pole odejmujesz od którego
Nie rozumiem ,jakie pole odejmujesz od którego  Uporządkuje swoja metodę
Uporządkuje swoja metodę  D1:
0≤x≤2
x2≤y≤2x2
D2:
2≤x≤2√2
x2≤y≤8
D1:
0≤x≤2
x2≤y≤2x2
D2:
2≤x≤2√2
x2≤y≤8

 OKI
OKI
 Coś mi sie nie zgadzało z tymi granicami całkowania
Coś mi sie nie zgadzało z tymi granicami całkowania  Moje uporządkowanie jest dobre?
Moje uporządkowanie jest dobre?

 A jakbym chciał względem OY to bym wział :
A jakbym chciał względem OY to bym wział :
 Więc odpada liczenie względem OY?
Więc odpada liczenie względem OY?
 czemu ty się tak upierasz przy tym y
całka od 0 do 1 z arcctg(x) − arctg(x)
czemu ty się tak upierasz przy tym y
całka od 0 do 1 z arcctg(x) − arctg(x)






 Ja to jestem....szalony
Ja to jestem....szalony  ale tak
ale tak


