Geometria analityczna
Fos: Prosze o pomoc w rozwiazaniu zadania.
Dla jakich wartości parametru m punkt przeciecia prostych y=mx+2 oraz x+my−1=0 należy do
prostokąta o wierzchołkach A(−2,1) B(−2,−1) C(1,−1), D(1,1).
A wiec tak:
Narysowałem ten prostokat i ograniczylem:
−2≤x≤1
−1≤y≤1
Nie wiem jak z ukłdau rownan mam kolejno wyznaczyc x i y tak zeby moc podstawic do warunkow z
poczatku zadania
3 mar 13:20
J:
y − mx = 2
my + x = 1
teraz wyznaczniki , potem podstawiasz x i y do warunków
3 mar 13:33
Fos: | | −2m+1 | | m+2 | |
wyszło mi x= |
| i y= |
| teraz wystarczy to podstawic do warnków i wziąć |
| | m2+1 | | m2+1 | |
z nich część wspólną?
3 mar 13:54
J:
tak
3 mar 13:55
Fos: a przy takim zadaniu? Dla jakich wartości parametru m prosta y=mx+m+1 ma dokładnie jeden punkt
wspolny z odcinkiem łączacym punkty A(1,0) i B (0,2)?
tez sie nad nim glowie

3 mar 17:17
Fos: tak samo jak wczesniej trzeba postepowac?
3 mar 17:18
Qulka:
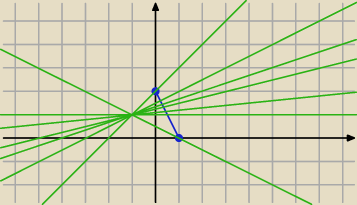
3 mar 17:25
Qulka: m∊<−0,5;1>
3 mar 17:25
Fos: nie czaje za bardzo tego rysunki

3 mar 17:38
Fos: Zrobilem w ten sposób jak wcześniej. Ograniczyłem x i y odcinka.
0≤x≤1 i 0≤y≤2
potem z układu dwoch równan
| | 1 | |
podstawiłem i obliczyłem ze dla x m∊ (−∞;− |
| > u <1;+∞) i dla y m∊ <0;1> i mi sie nie |
| | 2 | |
zgadza odpowiedz

3 mar 17:50
Fos: | | 1 | |
z tego by mi wynikało ze m=1, a w odpowiedzi mam podane m∊<− |
| ;1> |
| | 2 | |
3 mar 17:53
Qulka: bo masz układ
y+2x=2
y−mx=m+1
teraz policz
3 mar 21:44



