Odcinek łączący środki przekątnych i środki ramon świecznik: Czy w dowolnym trapezie odcinek łączący środki przekątnych pokrywa się z odcinkiem łączącym środki ramion? Jeśli tak to proszę wyjaśnienie lub dowód.

PW: Bez sensu. Środki przekątnych należą do wnętrza trapezu, a środki ramion − do brzegu trapezu. Jak mogłyby się pokrywać takie odcinki? Zadaj inaczej pytanie

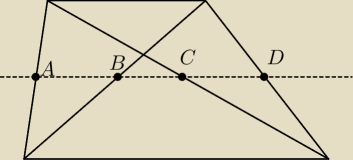
świecznik: Narysuje rysunek i sformułuje inaczej pytanie Punkty A i D są środkami ramion trapezu Punkty B i C są środkami przekątnych Czy te punkty leżą na jednej prostej?

PW: Tak. Oznaczmy literami PQ końce dolnej podstawy, a literami RS − końce górnej. W trójkącie PQS punkty A i C są środkami boków. Na mocy znanego twierdzenia odcinek AC jest równoległy do podstawy PQ. Takich samych obserwacji można dokonać na temat punktów A i B należących do boków trójkąta RSP − są końcami odcinka równoległego do RS. Mamy więc: − przez punkt A przechodzą dwa odcinki AC i AB równoległe do podstaw trapezu − powiedzmy, oba są równoległe do PQ (relacja równoległości jest przechodnia). Z odpowiedniego pewnika geometrii euklidesowej wynika, że oba te odcinki leżą na jednej prostej (przez punkt A nienależący do prostej PQ przechodzi dokładnie jedna prosta równoległa do PQ). Należenie A, B i C do prostej równoległej do PQ jest udowodnione, wystarczy to samo pokazać "z drugiej strony trapezu" dla odcinków DC i DB, co już jest nudne.

świecznik: Dziękuje za pomoc

świecznik: Tak żebym się miął nauczkę na przyszłość zapytam Dlaczego pierwsze pytanie nie miało sensu? Czy uważasz że (na rysunku) odcinek BC nie pokrywa się z odcinkiem AD