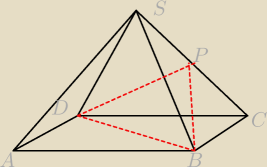
Dany jest ostrosłup prawidłowy czworokątny o podstawie ABCD Kamil: Dany jest ostrosłup prawidłowy czworokątny o podstawie ABCD i wierzchołku S ostrosłup ten przecięto płaszczyzną przechodzącą przez punkty B i D oraz przez punkt P będący środkiem krawędzi CS. Wykaż że jeśli trójkąt bdp jest równoboczny to stosunek długości krawędzi bocznej ostrosłupa do długości krawędzi podstawy jest równy 2√3 : √2

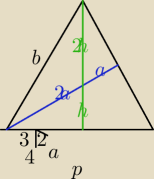Qulka: 4a²−9/8a²= 23/8 a² =h² b²=207/8a²+9/8a² = 27a² b=3√3 a

b		3√3 a		2√3
	=		=
p		3√2/2 a		√2

Qulka: ten trójkąt to widok z boku czyli Δ BCS Trójkąt BDP ma bok 3a więc p =3a/√2 (p−krawędź podstawy)

pigor: ... niech O − spodek wysokości ostrosłupa i |BD|=|DP|=|PB|=2a ⇒ |BC|=a√2 − dł. krawędzi podstawy oraz |OP|= ¹₂*2a√3=a√3 ⇒ jeśli np. |SC|=2k= 2|OP| ⇒

	2k		2*a√3
⇒ |SC| : |BC| =		=		= 2√3 : √2 ... c.n.w.
	a√2		a√2