analiza matematyczna SiA: Niech ktoś mądry pomoże z tym zadaniem Prosta k:y= ax+b, gdzie a>0, przechodząca przez punkt P(−1,2),odcina na osiach współrzędnych odcinki,których suma długości jest najmniejsza. Wyznacz równanie tej prostej.

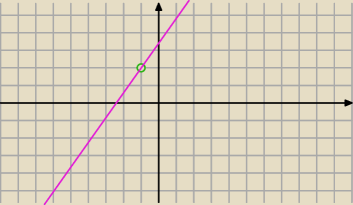===: Prosta przez P y−2=a(x+1) ⇒ y=ax+a+2 Pobawmy się równaniem w postaci odcinkowej ax−y=−(a+2)

ax		y		x		y
	+		=1 ⇒		+		=1
−(a+2)		a+2		−(a+2)   a		a+2

dla a>0

	a+2		a2+3a+2
mamy S=		+a+2=
	a		a

	(2a+3)a−a2−3a−2		a2−2
S'=		=
	a2		a2

S'=0 a²−2=0 zatem w warunkach zadania a=√2 czyli y=√2x+2+√2

===: możesz oczywiście bez tego równania −