twierdzenie Talesa Adrian: W trojkacie rownoramiennym ABC : ac = bc = 5, ab = 6. W jakiej odleglosci od prostej ab nalezy poprowadzic prosta k rownolegla do ab tak, aby poedzielila ona brzeg trojkata ABC na dwie czesci o rownych dlugosciach ? Wyliczam wysokosc trojkata, ktora wynosi 4. A prosta k dzieli moj bok ac na odcinki : 5−x, x. A

	5−x		4−y
wysokosc na odcinki 4−y, y. Ukladam proporcje :		=		i wychodzi mi ze :
	5		y

	4
x=		y
	5

Podstawiam potem di nast. Proporcji :

5−x		4−y
	=		. Po podstawieniu pod x. Otrzymuje ze y=1 a powinien sie rownac 0,8
x		y

Adrian: ?

prosta:

	5−x		4−y
a może:		=
	5		4

prosta:

	5
x=		y
	4

Adrian: no to już mam A teraz musze wyliczyć y lub x z innego równania i po podstawieniu ma być, że y = 0,8

prosta: trzeba jeszcze wziąć równanie na podział obwodu

Adrian: Czyli ?

prosta: co należy obliczyć? y?...twój opis oznaczeń nie jest jednoznaczny... oznacz na prawym ramieniu punkty A, A₁ ,C na lewym B, B₁, C ...na wysokości D, D₁, C. Czy y=|DD₁| ? x=|A₁C| ?

prosta: przy oznaczeniach: y=|DD₁| oraz x=|AA₁| mamy:

5−x		4−y
	=		i 2(5−x)=6+2x
5		4

	4
y=		x i x=1 ⇒ y=0,8
	5

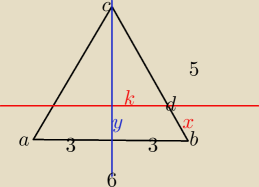
Adrian: niebieski kolor to wysokość, któa jest równa 4 a odcinek CK = 4−y a CB= 5 zaś CD= 5−x

Adrian: ?

prosta: nad rysunkiem rozwiązane już

Adrian: 2(5−x)=6+2x skąd to równanie ?

Adrian: Dobra już wiem. Dziękuję