matematykaszkolna.pl
Trygonometria Sara: Jaka jest największa wartość funkcji f(x) = sinx+cosx ?
2 mar 16:30
J:
 π 
sinx + cosx = √2sin(
+ x)
 4 
2 mar 16:32
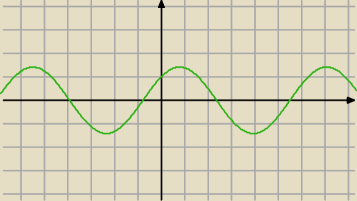
ax: rysunek
2 mar 16:32
Sara: A jak to obliczyć?
2 mar 16:33
J: jaka jest maksymalna i minimalna wartość funkcji sinus ?
2 mar 16:34
Sara: maksymalna 1, a minimalna −1
2 mar 16:36
J: to: √2*1 = ? √2*(−1) = ?
2 mar 16:38
PW:
√2 
= sin45° = cos45°
2 
można więc powiedzieć, że
 2 
f(x) =
(sinxcos45°+cosxsin45°),
 √2 
co po zastosowaniu wzoru na sumę sinusów daje f(x) = √2sin(x+45°)
2 mar 16:39
PW: Poprawka: wzoru na sinus sumy ("od prawej do lewej")emotka
2 mar 16:40
Chloe: A dlaczego w trzeciej linijce ten pierwiastek jest odwrócony?
2 mar 17:03
PW:
 √2 
Żeby się skróciło ze sztucznie dopisanymi
, czyli z sin45° i z cos45° (wymnóż i
 2 
sprawdź, że będzie f(x) = sinx + cosx, nic nie oszukali).
2 mar 17:20
prosta:
  π  
  π  
x+
−x
  2  
 
  π  
x−
+x
  2  
 
sinx+cosx=sinx+sin(
−x)=2sin
cos
  2   2   2  
  π  
  π  
2x−
  2  
  √2   π  
=2sin
cos
=2*
cos(x−
)=
  4   2   2   4 
  π  
= √2 cos(x−
)
  4 
2 mar 18:45
Sara: O teraz wszystko jasne, dziękuję bardzo emotka
2 mar 20:18