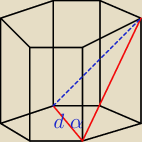
stereometria Frost: Zacząłem robić zadanko z gwiazdką z matmy i na razie moje pytanie brzmi czy dobrze oznaczyłem kąt? α− kąt pomiędzy najdłuższą przekątną ściany podstawy graniastosłupa prawidłowego sześciokątnego z przekątną ściany bocznej wychodzącej z tego samego wierzchołka Czy powstały trójkąt będzie prostokątny? Dla ciekawych: mam podane α oraz d i muszę obliczyć objętość i wyznaczyć α dla których zadanie ma rozwiązanie

prosta: nie jest prostokątny

Tadeusz: ... prostokątny nie jest !

prosta: można wbudować go w pewien trapez

Frost: co do trapezu to wiem już działam

Frost: Wyszło mi tak:

	3√3d3*√1+4cos2α
V=
	16cosα

a w książce mam odpowiedź:

	3√3d3		1
V=		*√		−1
	16		4cos2α

czy te odpowiedzi są równoważne ?

Metis: Podstaw sobie za d jakąś liczbę, jakiś kąt i podstaw....

prosta: raczej nie....w odp. odejmowanie a u ciebie suma

Frost: Można tylko za α. Dobra czyli nie są powinienem mieć 1−4cos²α czyli gdzieś błąd

Frost: Ok, znalazłem, przy liczeniu wysokości w pitagorasie przy przenoszeniu na drugą stronę znaku nie zmieniłem... Teraz myślę nad drugim podpunktem. Musze rozwiązać równanie V≠0 żeby wyznaczyć α?

Frost: Albo V>0 przy założeniu α<90

Frost: wyszło mi:

	1
cosα>		z V>0
	2

a w odp jest α∊(60^o,90^o)

Mila: Wyrażenie pod pierwiastkiem >0

1
	−1>0
4cos2α

1
	>1
4cos2α

1>4cos²α 4cos²α−1<0

	1
cos2α−		<0 ⇔
	4

	1		1
(cosα−		)*(cosα+		)<0 i cosα>0, α≠0
	2		2

	1
cosα>0 i cosα<
	2

	π		π
cosα<cos		i cosα>
	3		2

	π
cos(x) funkcja malejąca w przedziale (0,		)
	2

	π		π
α>		i α<
	3		2

Frost: Dzięki Mila! Wpadłem na to jak już leżałem w łóżku

Frost: Swoją droga z takim rozwiązaniem nierówności trygonometrycznych jeszcze się nie spotkałem