Kombinatoryka. Patryk: Witajcie, przygotowuję się do matury rozszerzonej i wszedłem w dział kombinatoryki i prawdopodobieństwa. Czasami nie wiem jakiego wzoru użyć. Macie jakieś rady do tego? Kiedy są wariacje, permutacje, a kiedy kombinacje?

5-latek: Poszukaj dzisiaj J Juz odpowiadal na to pytanie

Patryk: Dam może przykład. Każdy z sześciu skazanych ma być osadzonych w jednym z trzech zakładów karnych. Na ile sposobów można rozmieścić skazanych w tych trzech zakładach karnych? Odpowiedź to 3⁶. Mógłby mi ktoś wytłumaczyć dlaczego?

Patryk: Dzięki

J: ilość wszystkich funkcji określonych na zbiorze n elementowym, o wartościach w zbiorze k elementowym oblicz się ze wzoru: n^k

Patryk: To kolejny przykład. Dane są zbioty A = {1, 2, 3}, B={5, 6, 7, 8, 9} Ile jest wszystkich funkcji ze zbioru A w zbiór B? Dlaczego odpowiedzią jest 5³, a nie 3⁵?

J: bo ja źle napisałem .. ma być odwrotnie zbiór k jest dziedziną, a zbiór n przeciwdziedziną

J: w Twoim drugim przykładzie: n = 5 , k = 3

Patryk: A jak to rozróżnić? Miesza mi się

J: to wynika z treści ...funkcja odwzorowuje zbiór A w zbiór B . A jest dziedziną,B zbiorem wartości

Patryk: Może wróćmy do zadania o więźniach Naszym zbiorem skazanych będzie S = {A, B, C, D, E, F}, czyli 6 elementów. Zbiorem więzień będzie W = {1, 2, 3}, czyli 3 elementy. Funkcji ze zbioru W w zbiór S jest 3⁶, dobrze piszę? Bo do każdego z 3 więzień przypisuję każdego więźnia (coś takiego )

J: nie do końca ... .każdy więzień może trafić do jednego z trzech przykładowe układy: (1,1,2,2,1,3) (1,1,1,1,1,1) − wszyscy trafili do 1 ( 2,2,2,2,2,1) − ostatni do 1 ...itd

J: są to 6−cio elementowe wariacje z powtórzeniami zbioru 3 − elementowego: n^k

Patryk: Ok, to jest zrozumiałe, ale te oddziaływanie na zbiorach nadal mi nie wchodzi do głowy, a to wydaje się być podstawą

Patryk: Znalazłem definicję. Od razu lepiej Funkcją f ze zbioru X w zbiór Y nazywamy takie odwzorowanie, w którym każdemu elementowi ze zbioru X został przyporządkowany dokładnie jeden element ze zbioru Y.

Patryk: Dzięki J za pomoc, powalczę teraz trochę sam.

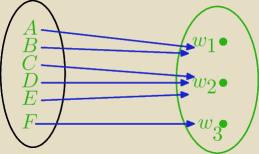
Mila: Każdemu więźniowi możesz przyporządkowąć jeden zakład karny na 3 sposoby. Czyli : 3*3*3*3*3*3=3⁶ pierwszy na 3 sposoby, drugi na 3 sposób, itd. Przykład: (w₁,w₁,w₂,w₂,w₂,w₃) jeden z możliwych 6−wyrazowych ciągów o wartościach {w₁,w₂,w₃}. Więzień A do w₁ Więzień B do w₁ Więzień C do w₂ .......... Wszystkich ciągów 6− wyrazowych o wartościach ze zbioru 3 −elementowego jest 3⁶.

Patryk: Dziękuję Mila. Pomożesz z tym? Dane są zbiory A = {1, 2, 3}, B={5, 6, 7, 8, 9}. Ile jest wszystkich funkcji rosnących ze zbioru A w zbiór B?

Patryk: Będzie coś takiego: Ciągi: (5,6,7,8,9), (5,7,8,9), (5,6,8,9), (5,6,7,9), (5,6,7,8)? Jeśli tak, to jak to obliczyć?

Patryk: Ale nie, bo... Przecież można 1 element przypisać, czyli będą to 3 elementowe ciągi, tak?

Patryk: Czyli (5,6,7) (5,6,8) (5,6,9) (5,7,8) (5,7,9) (5,8,9) (6,7,8) (6,7,9) (6,8,9) (7,8,9) I zgadza się z odpowiedzią, ale jest metoda żeby to obliczyć pbez rozpisywania?

Mila: |B|=5 Tyle, ile 3 elementowych podzbiorów zbioru B.

5 3		1
	=		*4*5=10
		2

Tyle samo jest funkcji malejących.

Mila: No i pięknie, że wypisałeś.

Patryk: Trochę nie rozumiem tego zapisu. Wygląda na to, że wybieramy 3 elementy ze zbioru 5 elementowego. W kombinacji chodzi tylko o to, ze wybieramy 3 różne elementy z tego zbioru, a kolejność tak jakby sami sobie możemy zrobić z tych liczb i z racji, że nie ma tam powtórek, zawsze istenieje możliwość ich ułożenia w ciągu rosnącym, tak?

	1
A co oznacza		*4*5?
	2

Patryk: A dobra, po prostu obliczyłaś w inny sposób niż ja, ja intuicyjnie liczę te z silnią i skracam co się da nie było tego pytania

Mila: 1) Tak, dobrze rozumujesz.

	5 3
2) To jest skrócone obliczenie wartości

5 3		5!		3!*4*5		4*5
	=		=		=
		3!*(5−2)!		3!*2		2

Patryk: Jeszcze raz dziękuję i pozdrawiam