nierówność
sevixy:
Rozwiaż nierówność:
√x2−4x+4+
√4x2+4x+1<4−x
Robię to tak:
składam to, co pod pierwiatskeim, tzn:
√(x−2)2+
√(2x+1)2<4−x
stąd:
|x−2|+|2x+1|<4−x
szukam miejsc zerowych:
x=2 x= −
12
Rozważam rozwiązania w 3 przedziałach, tzn
I. (−
∞,−
12)
II. <−
12)
III. <2,+
∞)
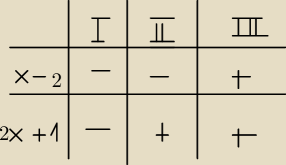
Rysuję pomocniczą tabelkę, następnie wyliczam przediały i wychodzi mi:
!. x∊(−
32,+
∞)
II. x∊(−
∞,
12)
III. x∊((−
∞,
54)
I teraz moje pytanie: wyznaczając sumę przedziałów wychodzi mi wynik błędny. Gdybym wyznaczyła
część wspólną tych przedziałów to wynik byłby prawidłowy. Jak więc powinno się to robić? A
moze gdzieś popełniłam błąd? proszę o wskazówki

 Rozwiaż nierówność:
√x2−4x+4+√4x2+4x+1<4−x
Robię to tak:
składam to, co pod pierwiatskeim, tzn:
√(x−2)2+√(2x+1)2<4−x
stąd:
|x−2|+|2x+1|<4−x
szukam miejsc zerowych:
x=2 x= −12
Rozważam rozwiązania w 3 przedziałach, tzn
I. (−∞,−12)
II. <−12)
III. <2,+∞)
Rysuję pomocniczą tabelkę, następnie wyliczam przediały i wychodzi mi:
!. x∊(−32,+∞)
II. x∊(−∞, 12)
III. x∊((−∞, 54)
I teraz moje pytanie: wyznaczając sumę przedziałów wychodzi mi wynik błędny. Gdybym wyznaczyła
część wspólną tych przedziałów to wynik byłby prawidłowy. Jak więc powinno się to robić? A
moze gdzieś popełniłam błąd? proszę o wskazówki
Rozwiaż nierówność:
√x2−4x+4+√4x2+4x+1<4−x
Robię to tak:
składam to, co pod pierwiatskeim, tzn:
√(x−2)2+√(2x+1)2<4−x
stąd:
|x−2|+|2x+1|<4−x
szukam miejsc zerowych:
x=2 x= −12
Rozważam rozwiązania w 3 przedziałach, tzn
I. (−∞,−12)
II. <−12)
III. <2,+∞)
Rysuję pomocniczą tabelkę, następnie wyliczam przediały i wychodzi mi:
!. x∊(−32,+∞)
II. x∊(−∞, 12)
III. x∊((−∞, 54)
I teraz moje pytanie: wyznaczając sumę przedziałów wychodzi mi wynik błędny. Gdybym wyznaczyła
część wspólną tych przedziałów to wynik byłby prawidłowy. Jak więc powinno się to robić? A
moze gdzieś popełniłam błąd? proszę o wskazówki