Geometria z f'(x); arkusz pr. Dżepetto 18: Dany jest trójkąt prostokątny o przyprostokątnych a i b oraz a+b=10. W trójkąt ten wpisano kwadrat w taki sposób, że dwa jego boki zawierają się w przyprostokątnych. Ustal długość boków trójkąta tak, aby wpisany w niego, w podany sposób, kwadrat miał największe pole. Rozrysowałem, oznaczyłem boki: a oraz 10−a; D= (0,10) Lecz dalej brakuje zamysłu. Myślałem coś o podobieństwie albo wzorze na pole trójkąta ale na myśleniu się skończyło.

Dżepetto 18: ?

Dżepetto 18: ktoś powalczy?

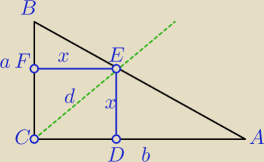
Mila: a+b=10 b=10−a ΔBFE∼ΔBCA⇔

a−x		a
	=		⇔
x		b

xa=ab−bx xa+bx=ab x*(a+b)=ab

	ab
x=
	a+b

	a*(10−a)
x=
	10

P=x²

	a2*(10−a)2
P(a)=
	100

Dalej poradzisz sobie?

Dżepetto 18: Pewnie, dalej już dam radę. Super! Dziękuję bardzo Mila

Eta: Prościej P−−− jest największe, jeżeli x−−−jest największe czyli gdy −a²+10a −−− osiąga maksimum i a∊(0,10) a to funkcja kwadratowa ⇒ że osiąga maksimum dla a=.........

Dżepetto 18: Teraz tylko kwestia odpowiedniego zapisu na maturze rozszerzonej Jak mówią moi nauczyciele "wpadniesz na pomysł ale i tak musisz wyrabiać sobie ramy, które potem wypełnisz tylko odpowiednimi danymi"− jeśli chodzi o zadanie za 6pkt

Eta: To jest zadanie na podstawę ( f. kwadratowa

Dżepetto 18: Niestety na podstawie nie ma pochodnych :c

Eta: Do znajdywania ekstremum dla f. kwadratowej nie są potrzebne pochodne!