tryg. początki: Proszę o pomoc : I 2sinx − 1 I < 1

początki: Czy to tak ? 2sinx−1 < 1 i −2sinx+1>1 2sin<2 −2sin>0 sin< 1 sin<0

początki: pomoże ktoś ?

początki: dobrze czy zle ?

Bogdan: |2sinx − 1| < 1 ⇒ −1 < 2sinx − 1 < 1 ⇒ 0 < 2sinx < 2 ⇒ 0 < sinx < 1 x∊(0 + k*2π, π + k*2π)

początki: jak mam określać ze x∊(0 + k*2π, π + k*2π)

Matgeo: Bogdan: wytłumaczysz ? jak mam określać ze x∊(0 + k*2π, π + k*2π)

Bogdan: k∊C, k jest liczbą całkowitą

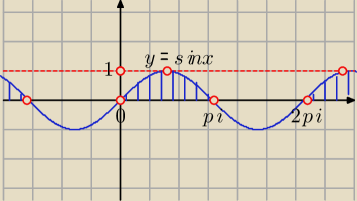
prosta: 1. Rysujesz sinusoidę 2. Rysujesz proste y=0 oraz y=1 i szukasz fragmentów sinusoidy pomiędzy nimi 3. Odczytujesz przedział argumentów związany z wyróżnionym fragmentem wykresu x∊(0,π) i uwzględniamy okres funkcji: x∊(0+2kπ,π+2kπ)

początki: dlaczego z z wyróżnionym fragmentem wykresu x∊(0,π) ?

początki: ?

prosta: x∊(0,π) ⇒ 0<sinx<1

prosta:

	1		1
drobna poprawka: x∊(0,		π)∪(		π,π)
	2		2