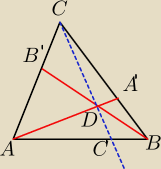
 W trójkącie ABC zaznaczono pkt A' na boku BC,tak że A'B:A'C= 1:2 i punkt B' na boku AC tak,że
B'A:B'C= 3:1.Odcinki AA' i BB' przecinają sie w punkcie D.
Prosta CD przecina odcinek AB w punkcie C'.
Pole trójkąta BA'D jest równe 14.
a) oblicz pole trójkąta ABC
b) oblicz stosunek CD : DC'
W trójkącie ABC zaznaczono pkt A' na boku BC,tak że A'B:A'C= 1:2 i punkt B' na boku AC tak,że
B'A:B'C= 3:1.Odcinki AA' i BB' przecinają sie w punkcie D.
Prosta CD przecina odcinek AB w punkcie C'.
Pole trójkąta BA'D jest równe 14.
a) oblicz pole trójkąta ABC
b) oblicz stosunek CD : DC'
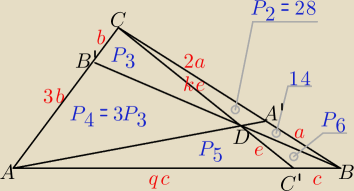 P − pole trójkąta ABC
P1 = 14, P2 = 2*P1 = 28, P4 = 3*P3
P − pole trójkąta ABC
P1 = 14, P2 = 2*P1 = 28, P4 = 3*P3
| 1 | 1 | 1 | ||||
P1 + P2 + P3 = | P ⇒ 42 + P3 = | P ⇒ P3 = | P − 42 | |||
| 4 | 4 | 4 |
| 2 | 2 | |||
P2 + P3 + P4 = | P ⇒ 28 + 4p3 = | P ⇒ P = 420 i P3 = 63 i P4 = 189 | ||
| 3 | 3 |
| q*c | a | b | 1 | ||||
* | * | = 1 ⇒ q* | = 1 ⇒ q = 6 | ||||
| c | 2a | 3b | 6 |
| 7 | ||
P3 + P4 = k*P5 ⇒ 252 = k*108 ⇒ k = | ||
| 3 |
| 7 | ||
Odp.: Pole trójkąta ABC jest równe 420, |CD| : |DC'| = | : 1 | |
| 3 |