Wyznacz objętość ostrosłupa prawidłowego czworokątnego, którego pole powierzchni M: Poszukuje pomocy w rozwiązaniu następującego zadania, będę niezmiernie wdzięczny jeżeli ktoś pokaże mi w jaki sposób to rozwiązać Wyznacz objętość ostrosłupa prawidłowego czworokątnego, którego pole powierzchni całkowitej jest równe S, a ściany boczne nachylone są do płaszczyzny podstawy pod kątem α.

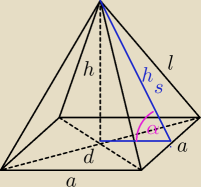dero2005: dane: S = a² + 2a*h_s

a   2
	= cosα
hs

	a
hs =
	2cosα

h² + (^a₂)² = h_s²

	a2		a2
h2 +		=
	4		4cos2α

	a2		a2		a2		1
h2 =		−		=		(		−1) =
	4cos2α		4		4		cos2α

	a2		1−cos2α		a2		sin2α		a2
=		(		) =		(		)=		*tg2α
	4		cos2α		4		cos2α		4

	a
h =		tgα
	2

	a
S = a2 + 2a*		tgα
	2

S = a²(1+tgα)

	S
a2 =
	1+tgα

	S
a = √
	1+tgα

	a2*h
V =
	3

dokończ