Prawdopodobieństwo warunkowe paula: Prawdopodobieństwo warunkowe Strzelec A trafia w cel z prawdopodobieństwem 0,7, strzelec B − z prawdopodobieństwem 0,6, a strzelec C − z prawdopodobieństwem 0,5. Strzelcy A, B, C oddali po jednych strzale do celu. Okazało się, że dwa pociski trafiły w cel. Co jest bardziej prawdopodobne: − strzelec C trafił w cel, czy też − strzelec C nie trafił w cel? Mógłby mnie ktoś jakoś naprowadzić albo rozwiązać krok po kroku?

paula: podbijam, może jednak ktoś pomoże..

Kinia: Drzewkiem rozrysuj strzał każdego z nich i weź pod uwagę gałęzie z dwoma trafieniami. Robiłam to zadanie o ile dobrze pamiętam.

Kinia: W sensie jedno drzewko i strzał każdego strzelca po kolei

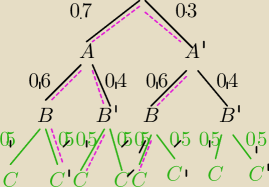
Mila: Zaznaczymy te ścieżki, gdzie cel został trafiony 2 razy. P(C/T₂)=0,7*0.4*0,5+0,3*0,6*0,5=0,14+0,09=0,23 strzelec C trafił w cel P(C'/T₂)=0,7*0,6*0,5=0,21 strzelec C nie trafił w cel

Kinia: Skoro trafia z prawdopodobieństwem 0,7 to nie trafia z prawdopodobieństwem 0.3... itd.

paula: hm.. a jak to rozpisać wzorami? bo drzewka nie miałam na zajęciach wprowadzanego...

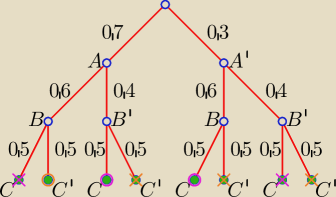
Dziadek Mróz: a) że C trafił: 1. A, B', C = 0.7 * 0.4 * 0.5 = 0.14 2. A', B, C = 0.3 * 0.6 * 0.5 = 0.09 b) że C nie trafił: 1. A, B, C' = 0.7 * 0.6 * 0.5 = 0.21

paula: dzięki, doszłam już o co chodzi z tymi drzewkami a żeby nie zaśmiecać nowym wątkiem, może ktoś mi z tym pomoże? Dane są dwa zbiory A = {1, 2, 3, ... , 2015, 2016} i B = {1,2,3,...,503,504}. Rzucamy sześcienną, symetryczną kostką do gry. Jeśli wypadną mniej niż trzy oczka losujemy liczbę c ze zbioru A,w przeciwnym wypadku losujemy liczbę c ze zbioru B. Oblicz prawdopodobieństwo zdarzenia, że liczba c² + 1 będzie podzielna przez 10. zaczęłam robić drzewkiem, ale stanęłam bo nie wiem jak znaleźć te liczby podzielne przez 10...

prosta: to te, których ostatnią cyfrą jest 3 lub 7

Qulka: tak

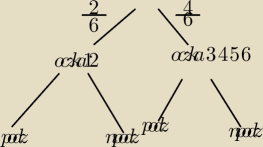
paula: nie wyszło mi.. robiłam następująco: ze zbioru A: jednocyfrowych: 2 dwucyfrowych: 9+9 trzycyfrowych: 90+90 czterocyfrowych: 100+100+2+1 (brałam pod uwagę te z 1 na początku, a później te z 2) w sumie 403 zbiór B: jednocyfrowe: 2 dwucyfrowe: 9+9 trzycyfrowe: 40+40+1 w sumie 101 i takie drzewko

paula: przepraszam ale nie wiem jak rysuje się drzewka tutaj później pomnożyłam 2/6 * 403/2016 + 3/6 * 101/504 = 1009/6048, a odpowiedź jest inna..

Mila: Jaka jest odpowiedź?

	2		1		4		2		3
Masz pomnożyć przez		=		i przez		=		( Ty mnożysz przez		)
	6		3		6		3		6

Ponadto zauważ , że 4*504=2016.

Mila: Ja liczyłam tak: A = {1, 2, 3, ... , 2015, 2016} W zbiorze A liczby z cyfrą jedności 3:( tworzą ciąg arytm o różnicy r=10) a₁=3 a_n=3+(n−1)*10=2013 2013−3=10n−10 2020=10n n=202 ==== ==== W zbiorze A liczby z cyfrą jedności 7:( tworzą ciąg arytm o różnicy r=10) b₁=7 b_n=7+(n−1)*10=2007 2007−7=10n−10 2010=10n n=201 ==== B = {1,2,3,...,503,504} W zbiorze B liczby z cyfrą jedności 3:( tworzą ciąg arytm o różnicy r=10) a₁=3 a_n=503 503=3+(n−1)*10 500=10n−10 n=51 W zbiorze liczby z cyfrą jedności 7:( tworzą ciąg arytm o różnicy r=10) b₁=7 b_n=497 497=7+(n−1)*10 490=10n−10 n=50

	1		202+201		2		50+51
P(A)=		*		+		*		=
	3		2016		3		504

	1		403		2		101		1211
=		*		+		*		=
	3		2016		3		504		6048

paula:

	173
Twoja odpowiedź jest dobra − po skróceniu przez 7 daje		czyli tyle ile w
	864

odpowiedziach. Wielkie dzięki! To podrzucam jeszcze jedno zadanko, które nie chce mi wyjść, może i z nim ktoś mi coś poradzi Zestaw tematów egzaminacyjnych składa się z 25 tematów z analizy, 35 tematów z geometrii i n tematów z rachunku prawdopodobieństwa. Z zestawu usunięto losowo jeden temat, a następnie z pozostałych wybrano w sposób losowy jeden temat. Oblicz n, jeśli wiadomo, że

	7
prawdopodobieństwo wylosowania tematu z rachunku prawdopodobieństwa jest równe		.
	27

prosta:

n		n−1		60		n		7
	*		+		*		=
60+n		59+n		60+n		59+n		27

n(n−1+60)		7
	=
(60+n)(59+n)		27

n(n+59)		7
	=
(60+n)(59+n)		27

n		7
	=
60+n		27

27n=420+7n 20n=420 n=21

paula: mógłbyś/mogłabyś wytłumaczyć pierwsze równanie?

mmmm: Jeżeli mamy prwdb warunkowe, to czy wystarczy w drzewku wykreślić C' i już ? Wg mnie drzewko się zmiania i prawdopodobieństwa na krawędziach też. Uważam, że wynik 0.23 (trafienie C) tyczy się zdanka, w którym nie ma zdania "Okazało się, że dwa pociski trafiły w cel." "

Marcin Bednara: Nie do końca zadanie zostało policzone. 0,23 to tylko część zadania (prawdopodobieństwo iloczynu). Trzeba jeszcze podzielić przez prawdopodobieństwo warunku, tj. 0,44