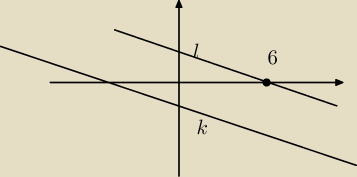
ble ble gabi: Na podstawie danych z rysunku poniżej wyznacz współczynniki A,B w równaniu ogólnym prostej l: Ax+By−12=0 k;x+3y+9=0 Nie wychodzi mi ni. Proste są chyba równoległe więc podstawiam za A 1 i punkt (6,0) ale i tak niezbyt dużo z tego wychodzi :c

gabi: pomocy ! :c

gabi:

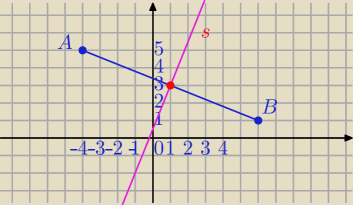
gabi: błagam bo zwariuje zaraz... i jeszcze takie zadanie ; wyznacz równanie ogólne symetralnej odcinka AB jeśli A(−4,5) B(6,1)

gabi: help

gabi: czemu nikt nie pomoże :c :c :c

5-latek: Pytanie : Co to jest symetralna odcinka ?

gabi: To prosta prostopadła do odcinka AB i przecinająca go w środku czyli zastosowałam wzór na środkową

gabi: tzn na środek odcinka

Mila: 1) k: x+3y+9=0 l ||k⇔ l: x+3y+C=0 i (6,0)∊l⇔6+3*0+C=0⇔C=−6 l: x+3y−6=0 /*2 l:2x+6y−12=0 spr. [1,3] ||[2,6] i 2*6+6*0−12=0⇔P=(6,0)∊l ================== 2) Symetralna AB, gdzie: A(−4,5) B(6,1) Symetralna odcinka to zbiór wszystkich punktów jednakowo odległych od końców odcinka. Zapisujemy tę własność: Niech P=(x,y) ∊symetralnej AB⇔ √(x+4)²+(y−5)²=√(x−6)²+(y−1)²⇔ x²+8x+16+y²−10y+25=x²−12x+36 +y²−2y+1 8x+16−10y+25=−12x+36−2y+1⇔ 20x−8y+4=0 /:4 5x−2y+1=0 postać ogólna równania symetralnej .

Mila: Gabi, jeśli chcesz korzystać z naszej pomocy , to nie używaj wulgaryzmów. Po prostu bądź damą.

5-latek: czemu od razu jebana ? Tak trzeba policzys wspolrzedne srodka odcinka AB wiec licz Nastepnie wyznaczyc wspolczynnik kierunkowy a prostej AB majac ten wspolczynnik masz juz wspolczynnik prostej prostopadlej a₁ do AB bo a*a₁=−1 to a₁=.... Napisz srownanie prostej prostopadlej do AB i przechodzacej przez srodek odcinka AB Zamien ja na postac ogolna

5-latek: Lub tez analezc wektor prostopadly do wektora [10 −4]

gabi: Oj przepraszam zdenerwowałam się trochę

gabi: a dlaczego w pierwszym to l takie wyszło? trzeba było wykonać m.i to równanie?− a1*b2+a2*b1=0

gabi: Za b też trzeba podstawiać ten sam współczynnik co w k?

gabi: halo halo nie zapominajcie o mnie

gabi: jak wyznaczyć ten współczynnik a? prostej AB

gabi: S mi wyszło [1;3] i potem ze wzoru na równanie kierunkowe prostej przechodzącej przez jeden punkt wyszło mi że współczynnik równał się 2/3 czy żle a ten wzór wyglądał tak y−a(x−x0)+y0 no to teraz spróbuje z jakiegoś magic wzoru na prostą przechodzącą przez dwa punkty czyli z tego (y2−y1)(x−x1)−(x2−x1)(y−y1)=0 ? hmm

gabi: wyszło mi −2x−5y+17 a ma być 5x−2y+1=o gdzie robie błąd?

gabi: :C

Mila: Nie ucz się schematów bez zrozumienia. Jeżeli masz prostą w postaci ogólnej: Ax+By+C=0 to każda prosta postaci: Ax+By+D=0 jest do niej równoległa, tylko wyrazem wolnym ( bez zmiennej) różnią się. Własnie z tego skorzystałam. II sposób: W Twoim zadaniu masz dany punkt (6,0) Podstawiasz do równania prostej l A*6+B*0−12=0 6A=12 A=2 Teraz korzystasz z warunku równoległości:A₁*B₂=A₂*B₁ k: x+3y+9=0 l: 2x+By−12=0 1*B=2*3 B=6 stąd: l: 2x+6y−12 Wyjaśnienie: Proste w postaci ogólnej : A₁x+B₁y+C₁=0 i A₂x+B₂y+C₂=0 są równoległe⇔ A₁*B₂−A₂*B₁=0 albo taki zapis: A₁*B₂=A₂*B₁

Mila: Teoria z przykładem. http://www.matematykam.pl/warunek_rownoleglosci.html

gabi: a co z tym drugim zadaniem bo to pierwsze już trochę ogarnełam

5-latek: Gabi Mila juz CI podala rozwiaznie tego zadania Ale skoro chcesz moim sposobem to zobacz Masz dwa punkty A(−4,5) i B(6,1) Wiemy ze wspolczynnik kierunkowy a prostej to jest tangens kata nachylenia prostej do osi OX

	y
Z trygonometri wiemy ze tgalfa =
	x

	y2−y1		6−(−4)		10		5
a wiec nasze a=		=		=		= −
	x2−x1		1−5		−4		2

	5
WIec wspolczynnik kierunkowy a prostej AB= −
	2

Obliczany wspolczynnik kierunkowy prostej a₁ prostej prostopadlej do AB

	−1		2
Warunek jest taki zeby proste byly prostopadle a*a1=−1 to a1=		to a1= −1*(−		=
	a		5

	2
	5

Znajac wspolczynnik kierunkowy prostej i punkt S przez ktory przechodzi napiszsemy jej rownanie y−y₀=a₁(x−x₀) to y=a₁(x−x₀)+y₀ masz wszystkie dane czyli a₁ i S=(1,3) czyli x₀=1 i y₀=3 podstawiaj i licz

5-latek: Potem postac kierunkowa zamien na ogolna Rozwiazanie Mili jest szybsze

Mila: Gabi przecież masz II rozwiązane 18:46. W drugim punkcie, z objaśnieniem. Jeśli tam czegoś nie rozumiesz to pytaj. Z Twojego wpisu rozumiem, że tego nie czytałaś.

5-latek: Nawet tak napisalem ze ma rozwiazane