ilustracja graficzna nierownosci Mefiu: Przedstaw ilustracje graficzną nierówności |x| + |y| < 2 jak zaczac to zadanie ? moglby mi ktos to wytlumaczyc ?

Mefiu: hmm..?

prosta: rozpatrzyć 4 przypadki znaków x oraz y ...odpowiednio opuścić wartości bezwzględne i narysować fragmenty figury

prosta: powstanie kwadrat (bez brzegu) o wierzchołkach (0,1) , (−1, 0) , (1, 0), (0,−1)

prosta:

	⎧	x≥0
1.	⎨	y≥0
	⎩	x+y<2

	⎧	x≥0
2.	⎨	y<0
	⎩	x−y<2

	⎧	x<0
3.	⎨	y≥0
	⎩	−x+y<2

	⎧	x<0
4.	⎨	y<0
	⎩	−x−y<2

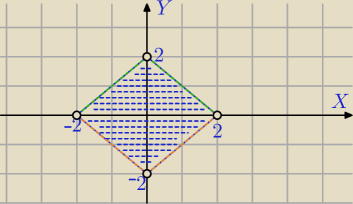
Mila: |y|<−|x|+2 ⇔ 1) Dla y≥0 ( nad osią OX) y<−|x|+2 punkty nad OX i pod wykresem y=−|x|+2 2)dla y<0 mamy taką nierówność: −y<−|x|+2⇔ y>|x|−2 punkty pod OX i nad wykresem y=|x|−2

Mefiu: a tak po kolei ? Bo zrobiłem tak: |x|+|y|<2 |x| = x dla x>0 |x| = −x dla x<0 |y| = y dla y>0 |y| = −y dla y<0 teraz licze : |x|+|y|<2 x+y<2 |x|+|y|<2 −x+y<2 y<2+x |x|+|y|<2 x+(−y)<2 −y<2−x /*(−1) y>−2+x |x|+|y|<2 −x−y<2 /*(−1) x−y>−2 no ale dalej nie wiem co zrobic ? nie wiem czy przybrac jakies parametry za to x i y, dowolne jakies czy co ? prosze o wytlumaczenie. dzieki

Mefiu: sie spoznilem z pytaniem kolejnym, a nie odswiezylem strony.

Mila: Przeczytaj co napisałam 16:46. Mam nadzieję, że wykres y=|x| − 2 i y=−|x|+2 umiesz narysować, wtedy zadanie jest proste.

Mefiu: ten wykres to biorąc punkty to wychodzi tak : x | 0 | 2 y=x−2 | −2 | 0 x | 2 | 4 | y=−|x|+2 | 0 | −2 | te kreski | to nie wartość bezwzględna tylko tabelka . Tak to ma wyglądać ?

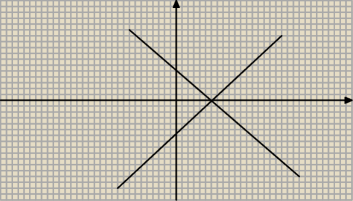
Mefiu: i jakich bym punktów nie wziął to i tak wykres wychodzi mniej więcej taki :

prosta: y=|x| wiadomo jak potem przesunięcie dwie jednostki w dół y=−|x| potem przesunięcie dwie jednostki w górę

5-latek: Teraz sie tego ucze Albo y=−|x| powstaje przez symetryczne odbicie wykresu y=|x| wzgleem osi Ox

Mefiu: moglbys to rozpisac ? nie pojmuje tego, dlatego prosze o wytlumaczenie. dzieki ;

prosta: https://matematykaszkolna.pl/strona/1374.html i ten wykres przesuwamy dwie jednostki w górę.

prosta: Mila ładnie to opisała w punkcie 2. W punkcie 1. odnosi się do wykresu funkcji y=|x| przesuniętego dwie jednostki w górę

prosta: możesz też rozpisywać po kolei: w I ćwiartce układu współrzędnych:

⎧	x≥0
⎨	y≥o	wtedy y<−x+2
⎩	x+y<2

otrzymujesz trójkąt prostokątny pod opisaną prostą w I ćwiartce układu

Mila: Mefiu, czy znasz definicję wartości bezwzględnej? Rysowaliście na lekcjach wykresy ? y=|x| y=|x|+1 y=|x|−1 itp.

prosta: w II ćwiartce układu współrzędnych:

⎧	x <0
⎨	y≥0	czyli y<x+2
⎩	−x +y<2

otrzymujesz trójkąt prostokątny pod opisaną prostą w II ćwiartce masz już "połowę" figury

Mila: Zostawiam Was, za dużo pomagających robi mętlik w głowie , bo każdy to robi w inny sposób. Powodzenia

prosta: Mefiu chyba już wylogował się

Mefiu: Owszem, troszkę się to namieszało. Zrobiłem tak, że wyszło jak mili, wykresy narysowałem te dwa pierwsze, jednakże nie wiem dlaczego we wzorze tak przekształciłem Bo zrobiłem tak , że : 1) y=−|x|+2 1a) y=−|x|−2 2) y=|x|−2 2a) y=|x|+2 Dążyłem, aby powstał ten romb taki jak u Mili Wyszło mi ładnie tak jak powinno, ale dalej nie rozymiem dlaczego trzeba było "przerobić" z −2 na +2

prosta: nic nie trzeba przerabiać: |x| +|y| <2 |y| <−|x| +2 i teraz : |y|=y dla y≥0 y <−|x| +2 nad osią oX obowiązuje wzór y =−|x| +2 i część płaszczyzny poniżej tego wykresu

Mila: Pokręciłeś to wszystko. Z definicji wartości bezwzględnej. |a|=a dla a≥0 |a|=−a dla a<0 Dlatego |8|=8 |−8|= −(−8)=8 |a|≥0 dla każdego a>0 Napisz po kolei małymi kroczkami, co mam wyjaśnić.

prosta: |y|<−|x| +2 −y<−|x| +2 , bo |y|=−y dla y<0 y>|x| −2 pod osią oX obowiązuje wzór y=|x| −2 i część płaszczyzny powyżej tego wykresu

prosta: ok...tym razem ja się wycofuję

Mila: Zostań prosta, myślałam, że odeszłaś od komputera.