proszę o rozwiązanie Michał: Podstawą ostrosłupa jest deltoid którego krótszy bok ma długość a a kąt ostry ma miarę 2α Każda krawędż boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem o mierze β Wyznacz objętość ostrosłupa

	a3 tgβ
wynik to V =
	6tgαsinα

	1
V =		*Pp*H
	3

jeżeli ABCD jest deltoidem to jego przekątne są prostopadłe AC ⊥ BD i DO = OB 0 ∊ DB AB = AD DC = BC = a przyjąłem że kąt DCB = 2α z Δ DOC CO = acosα OB = a sinα czyli DB = 2asinα

Michał: obliczyłem też H z Δ COS H = OC *tgβ = acosα*tgβ z ΔOAS

	H
obliczyłem OA =
	tgβ

ale po podstaieniu tych obliczeń nie otrzymałe poprawnej odpowiedzi

Michał: obliczyłem też P_p= P_ΔCBD + P_ΔDAB = a²sin2α

	1
V =		Pp*H
	3

	1		1
V =		* a2 sin2α*acosαtgβ =		* a3 sin2α*cosα*tgβ
	3		3

ale to nie jest zgodny z wynikiem może ktoś sprawdzi

Michał: ponawiam prośbę o sprawdzenie

Mila: Dlaczego H obliczyłeś z ΔCOS? Gdzie masz spodek wysokości ostrosłupa?

Michał: słusznie H to nie odcinek OS czy spodek wysokości nie będzie leżał podstawie na której da się opisać okrąg

Krab: Robię to samo zadanie i również mi nie wyszło, a nie wiem dlaczego moj wynik to:

	a3(cosα+sinα)*(2sinα)*tgβ*sinα
V=
	6

Nie widzę błędu niestety

Mila: Spodek wysokości leży w środku okręgu opisanego na tym deltoidzie. Trzeba obliczyc promień tego okręgu.

Mila: Krab jaką masz wysokość ostrosłupa?

Krab: Jak obliczyć długość |OA| gdzie O to punkt przecięcia przekatnych deltoidu a A wierzcholek najbardziej oddalony od niego ?

Krab: Wysokość zła niestety

Krab: Dziękujemy Mila! Dobranoc

Mila: 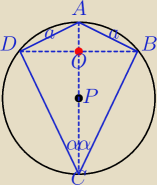Kąt 2α na dole, bo to ma być kąt ostry.

Krab: To wiele zmienia...

Krab: Teraz to juz nic nie wiem jak policzyć

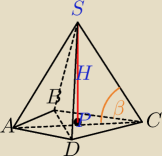
Mila: 1) czy wiesz dlaczego to taki deltoid? (wszystkie krawędzie boczne są nachylone pod tym samym kątem do płaszczyzny podstawy⇔ spodek wysokości tego ostrosłupa leży w środku okręgu opisanego na deltoidzie ) 2) Dlaczego nie wiesz co i jak liczyć? |AC|=2R (rysunek z 23:59)

a
	=2R
sinα

	a
R=
	2sinα

3) ΔABC− Δprostokątny ∡CAB=90−α

	|OB|		|OB|
sin(90−α)=		⇔cosα=		⇔
	a		a

|OB|=a* cosα

	a
PABCD=a* cosα*		⇔
	sinα

P_ABCD=a²*ctgα W ΔSPC:

	H
tgβ=		⇔
	|PC|

H=|PC|*tgβ⇔

	a
H=		*tgβ
	2sinα

	1		a
V=		*a2*ctgα*		*tgβ
	3		2sinα

	a3*ctgα*tgβ
V=
	6 sinα

====================

Michał: ja rozwiązałem z ΔABC prostokątny

	sinx		1		a
IAC I =		H = IPCI * tgβ I PC I =		IACI IBCI =
	a		2		tgα

	2asinα
IBOI = IBCI * sinα IDBI = 2* IBCI sinα IBDI =
	tgα

	1
Pp=		IACI*IBDI
	2

	a2
pp =
	tgα

	1
V =		Pp *H
	3

	1		a2		1		1		a*tgβ
V =		*		*H H = IPCI * tgβ =		*IACI tgβ =		*
	3		tgα		2		2		sinα

	1		a2		1		a*tgβ		a3*tgβ
V =		*		*		*		=
	3		tgα		2		sinα		6*tgα*sinα

Michał: dziękuję bardzo zanim ja napiszę to TY już wyślesz proszę o sprawdzenie bo skorzystałem z trójkąta

Mila: W |AC| chyba masz literówkę, odwrotnie?

Mila: Wysłałam, bo Krab napisał, że nie wie, jak liczyc. Teraz będę czekać na Twoje pytanie ( w innym zadaniu)

Krab: Teraz juz rozumiem, ale sprawiło mi to nie lada problem

Mila: To miło (Sz)Krabie.

Michał:

	sinα
słusznie w IACI jest literówka I ACI =
	a

Mila: Jak liczysz ten sinus?

Kinia:

	a
a ja mam |AC| =
	sinα

Kinia: także ten sam zbiór zadań

Mila: No i dobrze masz Kinia.

Kinia: o to miło, że znów błędu nie zrobiłam niektóre te zadania są dość wymagające

Kinia: nie chcę tak spamować, ale jestem zdesperowana po tak długim czasie robienia zadań, byłabyś tak dobra Mila i zerknęła na to: https://matematykaszkolna.pl/forum/282168.html