Dane są punkty Heiden: Dane są punkty A=(−3,−1), B=(4,−2). Na prostej l: y=−3x+5 znajdź taki punkt C, aby kąt ABC był prosty.

Tadeusz: ... poradzisz

Tadeusz: pewnie tylko wrzucił i poczeka na gotowca −

Qulka: albo tak jak Przemek..ogląda w tym czasie film a zadania same się robią

Heiden: no właśnie nie za bardzo bo rysunek to mniej więcej ogarnąłem coś więcej możesz podpowiedzieć Tadeusz?

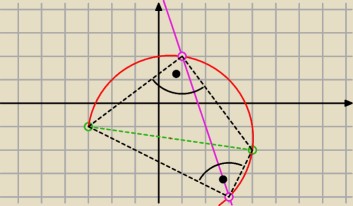
Mila: Może to pomoże? Kąt wpisany oparty na średnicy ( tu AB) jest kątem prostym.

Tadeusz: Zadanko te jak większość innych możesz zrobić na kilka sposobów. Jeśli wyznaczysz środek odcinka AB i z niego zatoczysz okrąg o promieniu równym połowie długości AB to każdy punkt leżący na tym okręgu z punktami A i B utworzą kąt prosty z wierzchołkiem w tym punkcie. Teraz pozostaje Ci tylko znaleźć punkty przecięcia tego okręgu daną prostą

Tadeusz: a jak chcesz się pobawić to możesz tak: Równanie pęku prostych przez punkt A=(−3, −1) to

	y+1
y+1=a1(x+3) ⇒ a1=
	x+3

Równanie pęku prostych przez punkt B=(4, −2) to

	y+2
y+2=a2(x−4) ⇒ a2=
	x−4

Teraz warunek prostopadłości

y+1		4−x
	=		... po wymnożeniu i przekształceniu do kanonicznej zobaczysz
x+3		y+2

równanie okręgu. Dalej przetniesz go swoją prostą i wyznaczysz oba punkty tj C₁ i C₂

Heiden: dzięki wielkie

Tadeusz: −

pigor: ..., dane są punkty A=(−3,−1), B=(4,−2). Na prostej l: y= −3x+5 znajdź taki punkt C, aby kąt ABC był prosty. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− widzę tonp. tak : z warunków zadania szukam punktu C=(x,y)= (x,−3x+5)= ? takiego, że |∡ABC|= 90^o ⇔ wektor BC ⊥ BA ⇔ [x−4,−3x+5+2] ⊥ [−3−4,−1+2] ⇔ ⇔ [x−4,−3x+7] ◯ [−7,1] = 0 ⇔ −7(x−4)+1(7−3x)= 0 ⇔ −10x+35= 0 ⇔ 2x= 7 ⇔ ⇔ x= 3,5= ⁷₂ ⇒ y= −3*⁷₂+¹⁰₂= −¹¹₂= −5,5 , zatem odp. C=(3.5, −5.5)= (⁷₂,−¹¹₂) − szukany punkt C . ...

Tadeusz: ... no tak .... a ja nie wiedzieć czemu zrobiłem dla ACB −:(

pigor: ..., zrobiłeś po prostu ... za dużo ; pozdrawiam ...