funkcja liniowa Paweł: Wyznacz takie wartości parametru m, aby prosta y=(2−m)x+1 miała punkt wspólny z odcinkiem o końcach A=(−1,4) i B=(2,3). Wychodzi z tego, że ten odcinek ma wzór y=0,125x+2,75 ale nie mam bladego pojęcia jak wyliczyć to m w tym wzorze y=(2−m)x+1 . Proszę o wytłumaczenie krok po kroku jak wyliczyć m. Dzięki z góry

Ja:

Tadeusz:

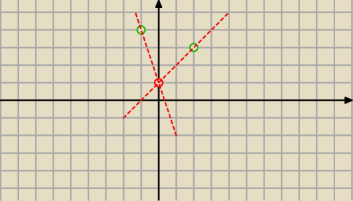
Paweł: Rozumiem, że ta 1 to jest z tej 1 ze wzoru, czyli y=(2−m)x +1 <− ta jedynka to jest (0,b), ale teraz jak to zapisac obliczenia do tego itp ?

Paweł: I teraz jak wyznaczyć m ?

Paweł: Może ktoś to wytłumaczyć ?

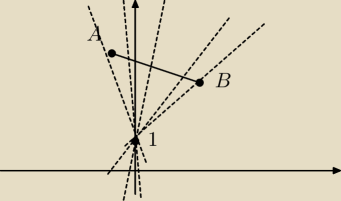
Tadeusz: y=(2−m)x +1 ta jedynka to ta jedynka czyli punkt C=(0, 1) teraz policz współczynniki kierunkowe prostych przez AC i przez BC

	4−1
a1=		=−3
	−1−0

	3−1
a2=		=1
	2−0

zatem ≤2−m≤

pigor: .. , a co z warunkiem 2−m≠0 ; chciałbym znać odp. do tego zadania, bo

pigor: ..., wyznacz takie wartości parametru m, aby prosta y=(2−m)x+1 miała punkt wspólny z odcinkiem o końcach A=(−1,4) i B=(2,3). −−−−−−−−−−−−−−−−−−−−−−−−− widzę to np. tak : I sposób : wektor AB= [3−1] ⇒ 1(x+1)+3(y−4)=0 ⇔ ⇔ x+3y−11= 0 − równanie prostej AB więc z warunków zadania szukasz takich wartości parametru m, że rozwiązania układu − punkty (x,y) przecięcia prostych y=(2−m)x+1 i x+3y−11=0 spełniają koniunkcje warunków −1< x <2 i 3< y <4 ; dla mnie za ... dużo roboty, ale widzę taki II sposób dany pęk prostych: y= (2−m)x+1 i (2−m)x+1=0 ⇔ x=⁻¹_2−m i 2−m≠0 ⇔ ⇔ x=¹_m−2 i (*)m≠2 − miejsce zerowe danej prostej ; prosta przez A=(−1,4) : 4=m−2+1 ⇒ m=5 ⇒ y= −3x+1 i −3x+1=0 ⇔ ⇔ 3x=1 ⇔ x=¹₃ − miejsce zerowe jednej z prostych pęku przez A ; oraz prosta przez B=(2,3) : 3=4−2m+1 ⇒ 2m=2 ⇔ m=1 ⇒ y= x+1 i x+1=0 ⇔ ⇔ x= −1 − miejsce zerowe prostej danego pęku przez punkt B ; −−−−−−−−−−−−−−−−−−−−−−−−−− zatem stąd i (*) warunki zadania spełniają nierówność podwójna: −1≤ ¹_m−2 ≤ ¹₃ /* 3(m−2)² ⇔ − 3(m−2)² ≤ 3(m−2) ≤ (m−2)² ⇔ ⇔ −3(m−2)²≤ 3(m−2) i 3(m−2)≤ (m−2)² ⇔ (m−2)²+(m−2) ≥0 i (m−2)²−3(m−2) ≥0 ⇔ ⇔ (m−2)(m−2+1) ≥0 i m−2(m−2−3) ≥0 ⇔ (m−2)(m−1) ≥0 i (m−2)(m−5) ≥0 ⇔ ⇔ (m ≤ 1 v m ≥ 2) i (m ≤ 2 v m ≥ 5), stąd i z (*) ⇔ m ≤1 v m ≥5 ⇔ ⇔ m∊(−∞;1> U <5;+∞). − szukany zbiór wartości parametru m. ...