Problem Predator: Mam problem. Dany jest prostokąt ABCD, w którym IABI:IADI=√2. Punkt S jest środkiem boku AB. Oblicz miarę kąta między prostymi AC i DS. Próbowałem wstawić rysunek ale mi nie wychodziło, miałem pomysł na to zadanie, ale chyba jest zły.

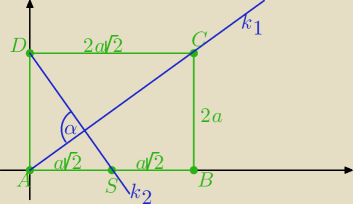
Bogdan: A(0, 0), S(a√2, 0), B(2a√2, 0), C(2a√2, 2a), D(0, 2a) a₁ − współczynnik kierunkowy prostej k₁ przechodzącej przez punkty A i C, a₂ − współczynnik kierunkowy prostej k₂ przechodzącej przez punkty D i S,

	2a		1		2a
a1 =		=		, a2 =		= −√2
	2a√2		√2		−a√2

a₁ * a₂ = −1 ⇒ k₁⊥k₂ ⇒ α = 90^o

Predator: Przepraszam za oznaczenia, a raczej ich brak. Mam obliczyć kąt w czerwnonym miesjcu. O ile dobrze zrozumiałem treść zadania. Próbowałem z tg obliczyc dwa inne kąty tego trójkąta. Boki oznaczyłem a√2 oraz przez samo a. Ale wyniki mi się nie zgadzały. Kąt ma 90.

Predator: Dzięki Mam pytanie, czy obliczając z funkcji trygonometrycznych może wyjśc mi dobry wynik ?

Bogdan: Pytanie jest zbyt ogólne.

Predator: Dobra próbowałem coś takiego. Patrząc na twój rysunek.

	2a
tgDSA=		=2/√2=1,41 z tablic tg55
	a√2

	2a
tgBAC=		=tg 0,7 z tablic tg45
	2a√2

Jak widać nie wychodzi dlaczego, czy nie moge tak robić ?

Bogdan:

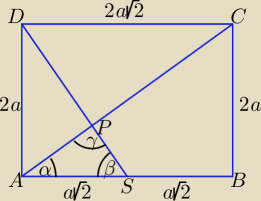
	2a
W trójkącie ASD: tgβ =		= √2
	a√2

	2a		1
W trójkącie ABC: tgα =		=
	2a√2		√2

	sinα		sinβ
tgα * tgβ = 1 ⇒		*		= 1 ⇒ cosα cosβ − sinα sinβ = 0
	cosα		cosβ

stąd cos(α + β) = cos90^o ⇒ α + β = 90^o i γ = 90^o.

Predator: Dzięki za opisanie, jednak twój pomysł jest łatwiejszy w realizacji.

prosta: ja liczyłabym z podobieństwa trójkątów APS i CDP i z tw. odwrotnego do tw. Pitagorasa

prosta: Uzależniłabym długości boków trójkąta APD od a i sprawdzała założenia tw. odwrotnego do tw. Pitagorasa

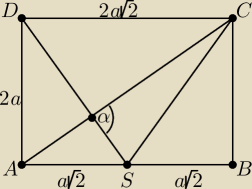Bogdan: Jeszcze inaczej: |AC| = √ 4a² + 8a² = 2a√3, |DS| = √ 4a² + 2a² = a√3*√2 Pole trapezu ASCD:

	1		1
P =		*2a*3a√2 = 3a2√2 i P =		*2a√3*a√3*√2*sinα = 3a2√2*sinα
	2		2

1 = sinα ⇒ α = 90^o