Twierdzenie Talesa Adrian:

	1		1		1
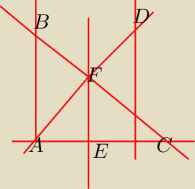
Proste AB, EF i CD na rysunku sa równoległe. Wykaż, ze		=		+
	|EF|		|AB|		|CD|

	EF		EC		EF
W podpowiedziach mam coś takiego : Dodaj stronami równości :		=		i
	AB		AC		CD

	AE
=
	AC

Czyli jak mam je dodać ?

Adrian: Gdy użyję tej proporcji z wskazówki No to mam :

EF		CE		EF		AE
	−		= 0 oraz		−		= 0 Czy mogę je przyrównać do siebie ?
AB		AC		CD		AC

Bo jeżeli w drugim równaniu zamiast przeniesienia prawej strony na lewo, przeniosę lewą na prawą, i przyrównaniu do siebie uzyskuję zupełnie inny wynik i co dziwne zgodny z odpowiedzią...

	EF		AE		AE		EF
Czyli zamiast		−		= 0 miałbym 0=		−
	CD		AC		AC		CD

Adrian: ?

J:

	EF		EF		EC		AE
Dodajemy stronami:		+		=		+
	AB		CD		AC		AC

	CD + AB		EC +AE
EF(		) =		= 1 ( bo EC + AE = AC)
	AB*CD		AC

1		1		1		1		CD + AB		CD + AB
	=		+		⇔		=		⇔ EF(		) = 1
EF		AB		CD		EF		AB*CD		AB*CD

c.n.w

Adrian: A jak pisałem ja, ze przyrównując je do zera ? to czemu wychodza dwa różne wyniki ?

J: bo to błąd ... jeżeli: a − b = 0 i c − d = 0 wcale nie oznacza ,że a = c i b = d

Adrian: Mi chodziło o coś takiego : Mamy układ równań a=b c=d a−b=0 c−d=0 co daje : a−b=c−d i nie mogę tak zrobić w tym przypadku ?

Adrian: ?