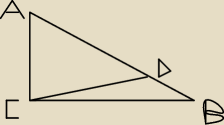
Oblicz pole BCD Agatonek123: W trójkącie ABC na rysunku kąt ACB jest prosty. Wiadomo przy tym, że CA=6 CB=8 AB=10. Punkt D leży na boku AB tak, że AD=7. Zatem pole BCD jest równe?

Patryk: Wyznacz sinus kąta CBD, oblicz długość DB (10−7), a na końcu wykorzystaj wzór na pole trójkąta z sinusa dla boków CB, DB i sinusa kąta CBD

Agatonek123: Niewiele mi to daje co napisałeś

Patryk: Ok, chwila

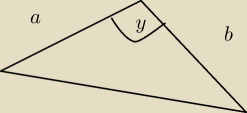
Patryk: Na początku oznaczmy kąt CBA=α.

	AC		6		3
Nasz trójkąt jest prostokątny, więc sinα=		=		=
	AB		10		5

Istnieje pewien wzór na obliczanie pola trójkąta mając dwa boki oraz kąt między nimi (patrz rysunek, ale zamiast γ jest y) , mianowicie:

	1
P=		* a * b * sinγ
	2

a = |CB|=8 b = |DB|=10−7=3 sinγ=sinα Czyli nasze pole:

	1		3		36		1
P=		* 8 * 3 *		=		=7
	2		5		5		5

Agatonek123: Dziękuje za pomoc

Patryk: