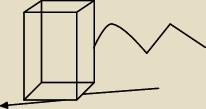
Długość przekątnej prostopadłościanu. kleszcz: Pole powierzchni całkowitej prostopadłościanu jest równe 198. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1:2:3. Oblicz długość przekątnej tego prostopadłościanu. Chciałbym o sprawdzenie, gdyż nie wiem czy dobrze mam. strzałka to bok 2x prosta to bok x ,,fala" to bok 3x d=√a²+b²+H² a=2x b=x H=c=3x 198=2(ab+bc+ac) 198=2(2x*x+x*3x+2x*3x) 198=2(2x²+3x²+6x²) 198=2*11x² 198=22x²/:22 x²=9 x=3 v x=−3∉D d=√3²+4*3²+9*3² d=p{9+4*9+9*9) d=√9+36+81 d=√126 d=3√14 Wszystko dobrze zrobione?

kleszcz: A nie się pomyliłem przy przekątnej d=p{4x²+x²+9x² d=√4*3²+3²+9*3² i wyjdzie to samo d=3√14 teraz dobrze ?

kleszcz: *d=√4x²+x²+9x²

Bogdan: Za dużo zapisów, wystarczy tak: k > 0 i 198 = 2*k*2k + 2*k*3k + 2*2k*3k ⇒ k² = 9 ⇒ k = 3 d = √k² + 4k² + 9k² = k√14 = 3√14

Eta: Dobrze tylko za bardzo "rozlazłe" w obliczeniach a=x, b=2x, c=3x , x>0 P_c=2(2x²+3x²+6x²)=198 ⇒ 11x²=99 ⇒ x=3 przekątna d ma długość d= √x²+4x²+9x²= √14x= 3√14

kleszcz: Rzeczywiście szybko zrobione .

kleszcz: ok, dzięki wam.

Eta: Na drowie

Eta: zdrowie