PW: Skoro nie daje Ci spokoju …
Zawsze trzeba zacząć od konstrukcji modelu matematycznego.
Czym jest losowanie z czwartej urny? − Wyborem jednej kuli spośród trzech, wylosowanie każdej z
| | 1 | |
nich ma jednakowe prawdopodobieństwo |
| . Jednak czwarta urna może być tworzona na wiele |
| | 3 | |
sposobów, można powiedzieć że tych "czwartych urn" jest wiele, i natrafienie na którąś z nich
miewa różne prawdopodobieństwo.
Popatrzmy, jakie mogą być te "czwarte urny":
U
4,1 = {b
1,b
2,z
3} (z pierwszej biała, z drugiej biała, z trzeciej zielona)
U
4,2 = {b
1,b
2,c
3} (z pierwszej biała, z drugiej biała, z trzeciej czarna)
U
4,3 = {b
1,z
2,c
3} (już dalej nie tłumaczymy, oznaczenia są zrozumiałe)
U
4,4 = {b
1,z
2,z
3}
U
4,5 = {c
1,z
2,c
3}
U
4,6 = {c
1,z
2,z
3}
U
4,7 = {c
1,b
2,c
3}
U
4,8 = {c
1,b
2,z
3}
Urn takich jest 8, tyle ile możliwości wybrania po jednym kolorze z trzech urn, które mają po
dwa rodzaje kolorów: 2
3 = 8.
Obliczenie prawdopodobieństw warunkowych P(C|U
4,j) nie sprawia trudności.
Zadanie możemy teraz sformułować następująco:
Jest 8 urn zdefiniowanych wyżej. Oblicz prawdopodobieństwo wylosowania czarnej kuli, jeżeli
losujemy jedną kulę z dowolnie wybranej urny U
4,1, ..., U{4,8}, a prawdopodobieństwa
wybrania poszczególnych urn są zakodowane sposobem losowania opisanym w pierwszych dwóch
zdaniach pierwotnego zadania.
Jednym zdaniem − jest to zadanie na zastosowanie
twierdzenia o prawdopodobieństwie
całkowitym (wzoru Bayesa), w którym prawdopodobieństwa poszczególnych urn są określone
przez prawdopodobieństwo w
przestrzeni 3 doświadczeń przebiegających niezależnie od
siebie (losowania z trzech pierwszych urn).
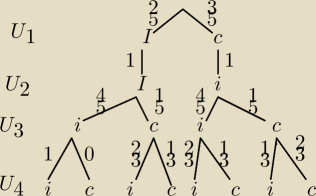c−czarna
i−inna
A−wylosowano czarną kulę