funkcje kwadratowe z parametrem Rinn: Dla jakich wartości parametru m dziedziną funkcji f(x)=√1−x − √−x²+2mx−4 jest zbiór jednoelementowy. Równianie ma jeden pierwiastek, gdy a>0 Δ=0 czy coś jeszcze? i jak obliczyć deltę z takiej funkcji

prosta: pierwszy pierwiastek ma sens dla x≤1. Dla drugiego trzeba tak ustalić m , by mniejsze miejsce zerowe funkcji kwadratowej było równe 1. Obliczmy: −1+2m−4=0 m=2,5

Rinn: z pewnością nie tak się to liczy

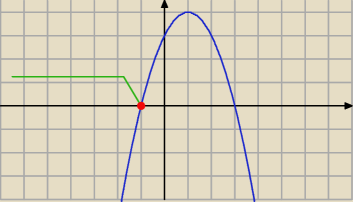
Mikołaj: Pomysł prostej był ok, tylko trzeba go trochę dopracować

prosta: to tylko rysunek do tego, co napisałam

Mikołaj: Albo nawet nie trzeba dopracowywać, bo jest ok No i mój rysunek jest do poprawy. Punkt wspólny to x=1, a ja zaznaczyłem x=−1. No ale już wiesz o co chodzi.

Rinn: trzeba rozpatrzyć kilka przypadków, tylko nie wiem jakich :v

Rinn: przynajmniej tak nam powiedziano, a zadanie jest za 6 pkt.. Jeśli to są całe obliczenia, to coś z punktacją musi być nie tak

prosta: dla wyznaczenia dziedziny należy zapisać dwa założenia: 1−x≥0 i −x²+2mx−4≥0 x≤1 x∊<x₁,x₂> ( o ile Δ≥0) ( gdyby Δ<0 to druga nierówność nie miałaby rozwiązań)

prosta: można trochę podrążyć temat :i uzasadnić szczegółowo swój punkt widzenia: dla m=−2,5: f(x)=√1−x−√−(x−1)(x−4)

Rinn: okej, dzięki

pigor: ..., jak się wyśpię ... wrócę tu., a teraz dobranoc..

pigor: ... , dla jakich wartości parametru m dziedziną funkcji f(x)= √1−x− √−x²+2mx−4 jest zbiór jednoelementowy ? −−−−−−−−−−−−−−−−−−−−−−−−−−−−− ..., naciskany przez ... moją Maję czas spełnić obietnicę, na to podobno 6 pkt. zadanie, a widzę to tak : funkcja f ma sens, czyli D_f: 1−x ≥0 i −x²+2mx−4≥0 ⇔ x≤1 i x²−2mx+4≤0, a ten układ warunków ma dokładnie jednoelementowy zbiór rozwiązań ⇔ ⇔ parabola g(x)= x²−2mx+4 ma : (1−no miejsce zerowe nie większe od 1) v (2 m.z.niezerowe x₁<x₂ i x₁=1) ⇔ ⇔ ( Δ=4m²−16=0 i x_w= −(−¹₂*2m) ≤1) v ( g(1)=0 i x_w >1) ⇔ ⇔ (m²=4 i m ≤1) v (1−2m+4=0 i m>1) ⇔ (|m|=2 i m ≤1) v (2m=5 i m>1) ⇔ ⇔ m= −2 v m= ⁵₂= 2,5 ⇔ m∊{−2, ⁵₂} . ....