Wektory Asia: Przez pkt A(2, −1,1) przez prowadzić prostą prostopadłą do wektorów a(−2, 1, −1) i b(3, 1, 2)

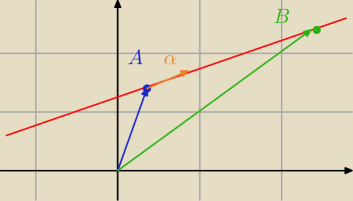
Ada: A dany punkt, B dowolny punkt na prostej. niebieski − wektor wodzący punktu A, zielony wektor wodzący punktu B. A(x₀,y₀,z₀) B(x,y,z) AB = (x−x₀,y−y₀, z−z₀) AB = − B + A ⇒ B = A − AB − równanie określające współrzędne punktu na prostej Ale możemy też przyjąć jakiś wektor α o kierunku prostej, wtedy AB = tα, t∊ℛ Wtedy: B = A + tα α − wektor kierunkowy prostej, musi być prostopadły do danych wektorów.

Mila: A(2, −1,1) a(−2, 1, −1) i b(3, 1, 2) k^→aXb jest prostopadły do obydwu wektorów, k^→[x,y,z] będzie wktorem kierunkowym szukanej prostej: i j k −2 1 −1 3 1 2 ========= k^→=[3,1,−5] Prosta :

x−2		y+1		z−1
	=		=
3		1		−5

Ada: Dzięki!

Asia: a jak jest wyliczony wektor k?

Asia: ktoś wie skąd k→[3,1,−5]?

Mila: Iloczyn wektorowy axb . Zobacz do notatek.