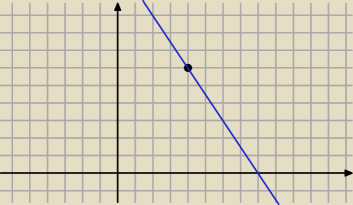
 y=ax+b
6=4a+b więc b=6−4a
Pole = b•(−b/a)/2 (tym razem dodatnie półosie więc a<0 b>0 więc −b/a >0 )
(6−4a)2/2a ma min dla a=−3/2
y=ax+b
6=4a+b więc b=6−4a
Pole = b•(−b/a)/2 (tym razem dodatnie półosie więc a<0 b>0 więc −b/a >0 )
(6−4a)2/2a ma min dla a=−3/2
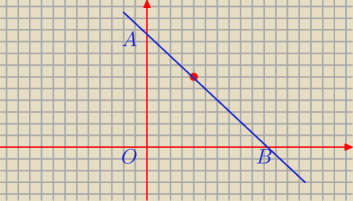 Prosta ma wzór f(x)=ax+b i punkt P należy do prostej
wychodzi, że f(x)=ax−4a+6
punkt A ma współrzędne (0, f(0)) natomiast punkt B (f(x)=0,0)
Prosta ma wzór f(x)=ax+b i punkt P należy do prostej
wychodzi, że f(x)=ax−4a+6
punkt A ma współrzędne (0, f(0)) natomiast punkt B (f(x)=0,0)
| 1 | 1 | |||
Pole liczysz jako | *|AO|*|OB|= | *f(0)*[f(x)=0] | ||
| 2 | 2 |
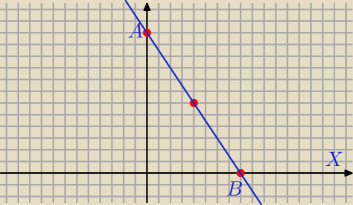 A=(0,m)
B=(n,0)
m,n>0
Równanie odcinkowe prostej.
A=(0,m)
B=(n,0)
m,n>0
Równanie odcinkowe prostej.
| x | y | ||
+ | =1 | ||
| n | m |
| 4 | 6 | ||
+ | =1⇔ | ||
| n | m |
| 4m+6n | |
=1 | |
| m*n |
| 6n | ||
m= | ||
| n−4 |
| 1 | ||
PΔ= | m*n⇔ | |
| 2 |
| 6n2 | ||
P(n)= | ||
| 2*(n−4) |
| 3n2 | ||
P(n)= | ||
| n−4 |
| 6n*(n−4)−3n2 | ||
P'(n)= | ||
| n−4 |
| 6n2−24n−3n2 | ||
P'(n)= | ||
| n−4 |
| 3n2−24n | ||
P'(n)= | ||
| n−4 |
| 6*8 | ||
m= | =12 | |
| 8−4 |
| x | y | ||
+ | =1 | ||
| 8 | 12 |
| −3 | ||
y=ax+12, b= | ||
| 2 |
| 3 | ||
y=− | x+12 | |
| 2 |