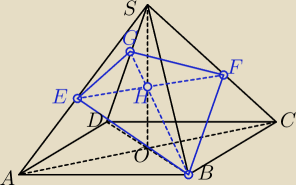
proszę o rysunek Michał: krawędzie boczne ostrosłupa prawidłowego czworokątnego ABCDS nachylone są do płaszczyzny jego podstawy ABCD pod kątem omierze 60⁰ .Długość krawędzi podstawy jest równa a Ostrosłup przecięto płaszczyzną przechodzącą przez wierzchołek B równoleglą do przekątnej AC i prostopadłą do krawędzi bocznej przeciwległej wierzchołkowi B

	√3a2
Udowodnij że pole otrzymanego przekroju jest równe
	3

Michał: czy to będzie deltoid

dero2005:

Michał:

	1		a√2
obliczyłem H =		d * cos600 ⇒ H =		H − wysokość ostrosłupa
	2		4

czy OH to połowa wysokości

dero2005: nie

dero2005:

	a√6
H =
	2

dero2005:

	a√6
GB =
	2

	3
EF =		a√2
	2

	GB*EF
P =		=
	2

Michał:

	aP{6}
jak obliczyłeś że H =		i dlaczego GB = H
	2

Michał:

	√6
żle zapisałem H =
	2

Michał:

	a√6
znowu zapisałem żle H =
	2

dero2005: ja nie napisałem że GB = H to jest przypadek H = SO

	a√2
OB =
	2

H
	= tg60o = √3 H =
OB

prosta: trójkąt BDS jest równoboczny , H jest punktem przecięcia wysokości tego trójkąta, więc dzieli wysokość w stosunku 1:2

prosta:

	2
stąd długość EF to		a√2
	3

Michał: według powyższego wzoru po wyliczeniu

	a2√2		√3a2
P=		a mamy udowodnić że P =
	4		3

dero2005: przepraszam za pomyłkę w przepisywaniu

	2
EF =		a√2
	3

Michał:

	a√6
teraz się zgadza interesuje mie dlaczego GB = OS=
	2

Michał: przepraszam że tak wcześniej zrozumiałem zapis to rzeczywiście literówka

dero2005: GB i OS to są wysokości trójkąta ABS. Ponieważ trójkąt jest równoboczny to wysokości są równe

Michał: chyba Δ DSB jeżeli jest on zgodny z rysunkiem 25 lut 18;06

dero2005: Masz rację . Δ DSB lub Δ ASC

Michał: dziękuję bardzo i przepraszam za niedogności przy pisaniu moim