Proste i okrąg Hue hue: Sieczna k: x−y+1=0 przecina okrąg o: x²+y²−6x−2y+1=0 w punktach A i B. Przez te punkty poprowadzono styczne do okręgu, które przecięły się w punkcie C. Napisz równanie okręgu opisanego na trójkącie ABC. Zacząłem od wyznaczenia środka okręgu, promienia, współrzędnych punktów A i B. Są to odpowiednio S(3,1),r=3 i A(0,1), B(3,4). Ustaliłem ogólne wzory prostych przechodzących przez punkty A i B ax−y+1=0 i ax−y+4−3a=0 Gdy próbuję obliczyć te styczne ciągle wychodzi sprzeczność, czy gdzieś mogłem zrobić błąd? Dzięki za każdą pomoc

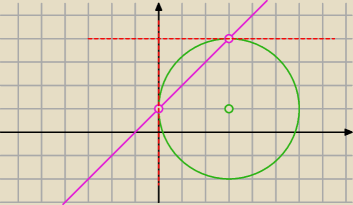
Tadeusz: ... widzisz dlaczego ?

Hue hue: No dobra okej, na rysunku wszystko widać, czyli gdzieś muszę mieć złe obliczenia bo jednak powinienem to samo uzyskać licząc to( bez rysunki) Jesteś w stanie pomóc?

Tadeusz: chcesz policzyć a ... czyli tangens kąta Widzisz, że ten kąt ma 90^o .... a tg90^o ....

Hue hue: A no tak, zapomniałem, że a to też tangens danego kąta. Ale pomijając to, co należałoby zrobić, żeby obliczyć te styczne nie korzystając z rysunku?

Tadeusz: dalej nie rozumiesz tg90^o nie istnieje więc jak to chcesz obliczyć Chcesz wyznaczyć równanie stycznej jako funkcji ... tyle że x=0 funkcją nie jest

Hue hue: No możliwe, że trochę się gubię, ale chodzi mi o to w takim razie, jak zapisać styczne, nie ma innej możliwości niż z rysunku, no bo okej, tu widać y=0 i x=4. Czy coś źle myślę? Chciałbym to zrozumieć a lekko się zagubiłem.

prosta: trochę jak armata na mrówkę: bierzemy równanie ogólne prostej : współczynniki A,B,C....powinno wyjść

prosta: albo: jest równanie stycznej w punkcie należącym do okręgu.....podobne do równania okręgu.

prosta: (x−a)(x_o−a)+(y−b)(y_o−b)=r² (x−3)(3−3)+(y−1)(4−1)=3² 3(y−1)=9 y=4

Hue hue: Dzięki, człowiek czasami tak się zamota, że 2+2 staje się trudne. Szczególnie jeszcze po ciężkim dniu.