geometria, zadanie Magda: Dwa okręgi przecinają się w punktach M i K. Przez punkt M poprowadzono prostą przecinającą te okręgi w punktach A i B (A≠M≠B), a przez punkt K prostą przecinającą okręgi w punktach D i C (C≠K≠D), przy czym odcinek AB nie przecina odcinka CD. Udowodnij, że czworokąt ABCD jest trapezem.

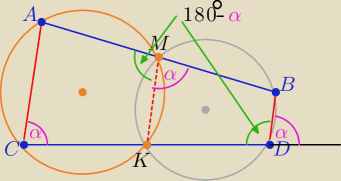
Eta: Patrząc na ten rys. napisz odpowiednie uzasadnienie ................. kończąc : odcinki AC i BD są nachylone do prostej AB pod tym samym kątem zatem AC∥BD czyli czworokąt ABCD jest trapezem

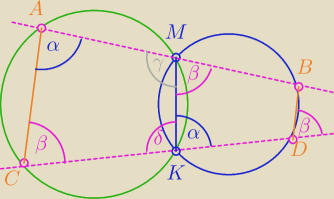
Tadeusz: Dowód sprowadza się do wykazania, że AC i BD są równoległe. Wykorzystaj zależność kątów czworokąta na którym można opisać okrąg https://matematykaszkolna.pl/strona/872.html δ=180−α to kąt przyległy znów α ....dalej poradzisz−

Eta:

Tadeusz: −