Geometria na płaszczyźnie kartezjańskiej
Michał:
Witam,
Mam problem z zadankiem z geometrii na płaszczyźnie kartezjańskiej. Nie wiem kompletnie jak je
zrobić, szukałem w tablicach, sam długo myślałem, ale pusta w głowie, nie mam pojęcia.
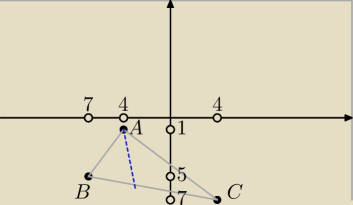
Dany jest trójkąt o wierzchołkach:
A=(−4,−1)
B=(−7,−5)
C=(4,−7)
Oblicz długość odcinka AD dwusiecznej kąta przy wierzchołku A.
A drugie to.
| | √3 | |
Znajdź kąt α pomiędzy prostymi y=x+2 oraz y= |
| x+1. Zapisz tgα. |
| | 3 | |
Dziękuję ślicznie za pomoc z góry.

24 lut 17:54
Michał: 
24 lut 19:59
24 lut 20:20
Michał: nigdy tego wzoru nie dojrzałem w tablicach i nigdy go nie używałem. Dzięki @Mila!
24 lut 20:35
PW: Z zadaniami z geometrii analitycznej jest na ogół tak, że jeśli nie znasz odpowiedzi w
terminach "zwykłej geometrii", to i sposobami analitycznymi też trudno.
Do zadania 1. mam propozycję: punkty dwusiecznej są jednakowo oddalone od obu ramion kąta.
Trzeba by więc napisać dla szukanego punktu (x0, y0) wzory na odległości od prostych AC i
AB.
Punkt (x0, y0) należy do odcinka BC, więc spełnia równanie prostej BC. Rozwiązując taki układ
równań może dojdziemy do (x0, y0).
Nie wiem, czy ta propozycja nie jest zbyt pracochłonna.
24 lut 20:40
Mila:
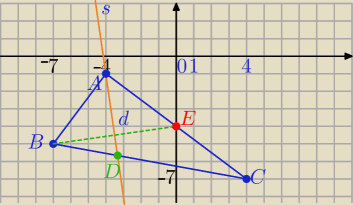
A=(−4,−1)
B=(−7,−5)
C=(4,−7)
|AB|=5
|AC|=10
AB
→[−3,−4]
AC
→[8,−6]
|u|=|AB|
A=(−4−1)→T{[4,−3]→E=(0,−4)
ΔBEA jest trójkatem równoramiennym, zatem symetralna BE będzie dwusieczną kąta BAE
P(a,b) − punkt dwusiecznej , jest jednakowo odległy od końców odcinka BE
√(a+7)2+(b+5)2=
√(a−0)2+(b+4)2⇔
b=−7a−29
Dwusieczna ∡BAC : y=−7x−29
Dalej poradzisz sobie?
24 lut 20:49
prosta: a można tak po prostu policzyć długości boków trójkąta i zastosować tw. cosinusów dla kątów α i
180o−α przy wierzchołku D ?
Do tego tw. o dwusiecznej...
Też trochę pracy.
24 lut 20:58
Michał: Tak, dziekuję. Potem może wstawię odpowiedź bo teraz jeszcze męczę coś innego.
@PW
No właśnie geometria pod każdą postacią to taka moja pięta. Matematyki rozszerzonej uczę
się(wcześniej tylko siedziałem na lekcjach) od pół roku i właśnie na geometrię potrzebuję
więcej czasu niż poświęciłem dotychczas.
24 lut 21:03
 Witam,
Mam problem z zadankiem z geometrii na płaszczyźnie kartezjańskiej. Nie wiem kompletnie jak je
zrobić, szukałem w tablicach, sam długo myślałem, ale pusta w głowie, nie mam pojęcia.
Dany jest trójkąt o wierzchołkach:
A=(−4,−1)
B=(−7,−5)
C=(4,−7)
Oblicz długość odcinka AD dwusiecznej kąta przy wierzchołku A.
A drugie to.
Witam,
Mam problem z zadankiem z geometrii na płaszczyźnie kartezjańskiej. Nie wiem kompletnie jak je
zrobić, szukałem w tablicach, sam długo myślałem, ale pusta w głowie, nie mam pojęcia.
Dany jest trójkąt o wierzchołkach:
A=(−4,−1)
B=(−7,−5)
C=(4,−7)
Oblicz długość odcinka AD dwusiecznej kąta przy wierzchołku A.
A drugie to.


 A=(−4,−1)
B=(−7,−5)
C=(4,−7)
|AB|=5
|AC|=10
AB→[−3,−4]
AC→[8,−6]
A=(−4,−1)
B=(−7,−5)
C=(4,−7)
|AB|=5
|AC|=10
AB→[−3,−4]
AC→[8,−6]