stożek
ola: Tworzaca stozka widac ze srodka kuli wpisanej w ten stozek pod katem o mierze � . Wyznacz
stosunek objetosci kuli do objetosci stozka.
(a) 4 ctg3α ctg2α
(b) 2 ctg3α ctg2α
(c) 4 ctg3α cos 2α
(d) −4 ctg3α ctg2α
24 lut 15:44
prosta: tworzącej nie widać
28 lut 15:53
Eta:
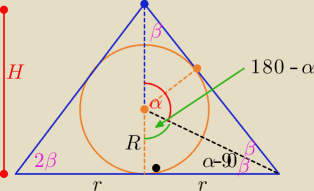
r−− dł. promienia podstawy stożka
R−− dł. promienia kuli wpisanej w stożek
α −− kąt widzenia tworzącej stożka ze środka kuli
2β= 2α−180
o
w zapisie pomijam symbol stopnia)
| R | | H | |
| =tg(α−90) ⇒ R= − r*ctgα i |
| = tg(2α−180) ⇒ H= r*tg2α |
| r | | r | |
| | 4 | | 1 | | 1 | |
V(kuli) = |
| πR3 , V(stożka) = |
| πr2*H= |
| πr3*tg2α |
| | 3 | | 3 | | 3 | |
| Vk | | 4*(−r*ctgα)3 | |
| = ......... = |
| = −4ctg3α*ctg2α |
| Vs | | r3*tg2α | |
odp: D)
28 lut 16:35
Eta:
Poprawiam chochlika (przy wierzchołku stożka pomyłkowo wpisał mi się kąt β
28 lut 16:39
 r−− dł. promienia podstawy stożka
R−− dł. promienia kuli wpisanej w stożek
α −− kąt widzenia tworzącej stożka ze środka kuli
2β= 2α−180o
w zapisie pomijam symbol stopnia)
r−− dł. promienia podstawy stożka
R−− dł. promienia kuli wpisanej w stożek
α −− kąt widzenia tworzącej stożka ze środka kuli
2β= 2α−180o
w zapisie pomijam symbol stopnia)